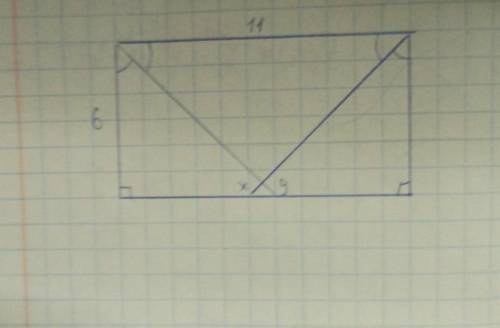
решить задачу

найти расстояние от x до y

1

Объяснение:

1) Докажем, что данный четырёхугольник является прямоугольником.

Согласно условию задачи:

углы при нижнем основании - прямые;

4 угла при верхнем основании равны между собой и равны:

180 : 4 = 45°, в силу чего наклонные прямые являются биссектрисами верхних углов, а каждый из них равен:

45 + 45 = 90°.

В прямоугольнике противоположные стороны равны.

Следовательно, нижнее основание четырёхугольника равно 11.

2) Биссектрисы прямых углов делят их на 2 равных угла, каждый по 45°; следовательно, треугольники, прилегающие к боковым сторонам, является равнобедренными, и их нижние стороны равны 6.

3) Общая длина оснований этих треугольников составляет:

6 + 6 = 12

4) Полагая, что точки х и у, принадлежат нижней стороне прямоугольника, найдём расстояние между ними:

12 - 11 = 1

ответ: 1