1. Геометрия
  2. Решить задачи на фото

Решить задачи на фото Подробно. Если не знаете, не отвечайте.

tgeibdizn tgeibdizn    3   06.04.2020 14:17    0

Ответы
VADIMECHE VADIMECHE  12.10.2020 17:58
Решение:Задача #1.

Чтобы найти катет, не лежащий напротив угла в 30°, нужно найти сначала первый катет, равный половине гипотенузы. Т.е. катет AC, лежащий напротив угла B в 30°, равен половине гипотенузы.

AC=AB\cfrac{1}{2}=6\cdot \cfrac{1}{2}=\cfrac{6}{2}=3

Теперь найдём второй катет по теореме Пифагора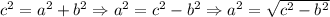 c^2=a^2+b^2 \Rightarrow a^2=c^2-b^2 \Rightarrow a^2=\sqrt{c^2-b^2}.

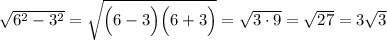
\sqrt{6^2-3^2}=\sqrt{\Big(6-3\Big)\Big(6+3\Big)}=\sqrt{3\cdot 9}=\sqrt{27}=3\sqrt{3}

ответ:  \boxed{\bf 3\sqrt{3}}.Задача #2.

Обозначим тр-к MOP, где PO - длина; PM - расстояние от самой постройки до основания лестницы; OM - расстояние от верхушки лестницы до её начала. Предлагаю сначала найти OM по свойству катета, лежащего напротив угла в 30°.

OM = PO\cfrac{1}{2}=10\cdot\cfrac{1}{2} = \cfrac{10}{2}=5 (метров).

Теперь найдём PM по теореме Пифагора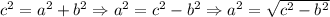 c^2=a^2+b^2 \Rightarrow a^2=c^2-b^2 \Rightarrow a^2=\sqrt{c^2-b^2}.

\sqrt{10^2-5^2}=\sqrt{\Big(10-5\Big)\Big(10+5\Big)}=\sqrt{5\cdot15}=\sqrt{75}=5\sqrt{3} (метров).

Но можно было найти катет PM по косинусу угла MPO.

ответ:   \boxed{\bf 5} (метров); \boxed{\bf 5\sqrt{3}} (метров).Задача #3.

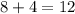Пусть a метров равна высота. Человек имеет рост 1,7 метров, а расстояние от фонарика до тени человека равно 8+4=12 шагов. Т.к. тр-ки подобны, то их стороны пропорциональны. Т.е. сторона PB △PBA пропорциональна стороне MC △MCA, а также сторона AB △PBA пропорциональна стороне CA △MCA. Т.е. решим задачу пропорцией.

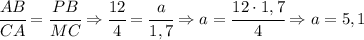\cfrac{AB}{CA}=\cfrac{PB}{MC} \Rightarrow \cfrac{12}{4}=\cfrac{a}{1,7} \Rightarrow a=\cfrac{12\cdot1,7}{4} \Rightarrow a=5,1 (метров).

ответ:   \boxed{\bf 5,1} (метров).
Решить задачи на фото Подробно. Если не знаете, не отвечайте.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
elenakosolapova elenakosolapova  10.09.2020 23:54
Решить задачу. Площадь параллелограмма равна 84 см², а одна из его сторон -12 см. Найдите высоту параллелограмма, проведенную к этой стороне...
oleca3 oleca3  10.09.2020 23:54
Периметр треугольника равен 228 мм. Длина первой стороны на 14 мм больше длины второй стороны, а длина третей стороны - на 12 мм больше длиины первой стороны. Определите...
ванёк10062005 ванёк10062005  10.09.2020 00:19
около прямоугольного треугольника абс с прямым углом с,описана окружностьнайдитё радиус окружности если ас 18 см​...
глупенький11 глупенький11  10.09.2020 00:20
Нарисуйте тетраэдр PABC Укажите его грань равную грани PAB, если а) PA=PC, AB=BC=CAб) PA=BC, PB=AC, PC=ABв) PA=PB=AC, PC=AB=BCВыберите сами другую грань тетраэдра и...
Bandit009 Bandit009  09.09.2020 23:16
СҰРАҚТАР 1. Жай тұйық сынық сызықтың анықтамасын беріңдер.2. Қандай фигура көпбұрыш деп аталады?3. Қандай көпбұрыш дөңес деп аталады? Мысал келтіріңдер.4. Дөңес п-бұрыштың...
GAMAEW66 GAMAEW66  08.02.2021 21:15
На биссектрисе угла B треугольника ABC отмечены точки E и F такие, что AB=BE и CB=BF. Докажите, что AF=CE....
shakurovagaliya shakurovagaliya  08.02.2021 21:15
БЫСТРЕЕ!Решите задачу по геометрии! Дано: тр-ник ABC, AN=NB BK=KC NK- средняя линия тр-ка ABC доказать: NK//AC NK=1/2AC Док-во:...
Neznat13 Neznat13  08.02.2021 21:11
Сторона трикутника дорівнює 4√2 см а прилеглі до неї кути дорівнюють 80 градусів 55 градусів. Знайдіть довжини дуг, на які вершини трикутника ділять описане навколо...
Trolololo09 Trolololo09  22.08.2019 04:10
Решить к гипотенузы прямоугольного треугольника прооведено высоту и медиану расстояние между основаниями которых равна 7 см.знайдить периметр треугольника, если медиана,...
ArtLeg ArtLeg  03.06.2019 05:30
Основания вс и ад трапеции авсд соответственно равны 1 и 100, а диагональ ас равна 10. докажите что треугольники вас и дса подобны...

Популярные вопросы