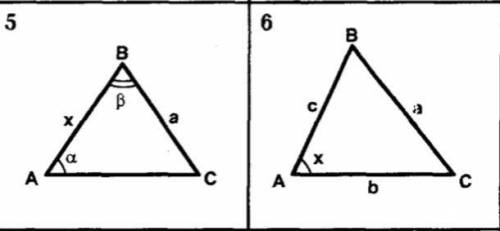
Решить задачи 5 и 6, найти x

Объяснение:

1) x/sin(180-(α+β)) = a/sin(α) => x = (a*sin(α+β))/(sin(α))

2) x = arccos( (a^2-b^2-c^2)/(-2*b*c) )

Задача 5:
Для решения этой задачи нам нужно выразить х в виде выражения.

Дано, что AC и BD - перпендикулярные диагонали прямоугольника ABCD.
Обозначим точку пересечения диагоналей как О.

Мы знаем, что в прямоугольнике противоположные стороны равны, поэтому AB = CD и AD = BC.

Также, в перпендикулярных треугольниках AOB и COD противоположные углы равны, поэтому ∠OAB = ∠OCD и ∠OBA = ∠OBC.

Мы можем использовать эти факты, чтобы выразить х в виде выражения.
Рассмотрим треугольник AOB:
Угол AOB равен 90 градусов (так как AC и BD - перпендикулярные диагонали), поэтому ∠OAB + ∠OBA + ∠OAB = 180 градусов.
Так как ∠OAB = ∠OBA, мы можем записать это как 2∠OAB + ∠OAB = 180 градусов.
Объединяя подобные элементы, получим 3∠OAB = 180 градусов.
Разделим обе стороны на 3, чтобы найти меру угла ∠OAB: ∠OAB = 180 градусов / 3 = 60 градусов.

Теперь рассмотрим треугольник COD:
Аналогично, угол COD равен 90 градусов.
Так как ∠OCD = ∠OAB (противоположные углы), мы можем записать ∠OCD = 60 градусов.

Осталось решить уравнение для нахождения x.
Так как ∠OCD является углом треугольника, равным 60 градусов, мы можем записать это как:
3x + 60 = 180.

Вычтем 60 из обеих сторон уравнения:
3x = 180 - 60,
3x = 120.

Разделим обе стороны на 3, чтобы найти значение x:
x = 120 / 3,
x = 40.

Таким образом, значение x равно 40.

Задача 6:
Для решения этой задачи нам также потребуется выразить х в виде выражения.

Нам дан треугольник ABC с углом C равным 95 градусов.
Обозначим точку пересечения отрезков AD и BE как O.

Мы знаем, что сумма углов в треугольнике равна 180 градусов, поэтому:
∠CAB + ∠ABC + ∠BCA = 180.

Мы также знаем, что угол A∠BCD равен 90 градусов (так как AD - высота треугольника ABC).

Таким образом, ∠DCB (треугольника DCB) равен 90 - 95 = -5 градусов (отрицательный угол).

Теперь рассмотрим треугольник AOD:
Угол AOD также равен 90 градусов.
Так как углы треугольника равны между собой, мы можем записать:
∠DOA = ∠DAC = ∠CAB = ∠BCD.

Так как у треугольника AOD только два угла, то ∠DOA + ∠ODA = 90 градусов.
Подставим ∠ODA = ∠DOA = ∠ABC = ∠CAB в это уравнение, и получим:
2∠DOA = 90 градусов.

Разделим обе стороны на 2, чтобы найти меру угла ∠DOA:
∠DOA = 90 градусов / 2 = 45 градусов.

Теперь решим уравнение для нахождения х.
Так как ∠DOA является углом треугольника, равным 45 градусов, мы можем записать это как:
3x + 45 = 180.

Вычтем 45 из обеих сторон уравнения:
3x = 180 - 45,
3x = 135.

Разделим обе стороны на 3, чтобы найти значение x:
x = 135 / 3,
x = 45.

Таким образом, значение x равно 45.