решить с пояснением, не только ответ Трапеция ABCD вписана в окружность (AD II BC), AB=13, BC=7, периметр 50. Найти:
1. CD и AD
2.среднюю линию трапеции
3. Площадь трапеции
4. tg/_BAD
5.cos /_ BCD
6.AC
7.радиус вписанной окружности
8.радиус описанной окружности

Трапеция ABCD вписана в окружность (AD II BC), AB=13, BC=7, периметр 50. Найти:   1. CD и AD  ;  2.среднюю линию трапеции  ;  3. Площадь трапеции  ;  4. tg∠BAD  ;   5.cos ∠BCD  ;  6.AC  ;  7.радиус вписанной окружности  ;  8.радиус описанной окружности.

Объяснение:

1) Описать окружность можно только около равнобедренной трапеции ⇒ CD=13 , Тогда AD=50-(2*13+7)=17.

2)Средняя линия равна полусумме оснований :  .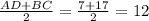

3) S (трапеции) =1/2*h*(a+b)  .Отложим от точки D отрезок DK=BC. Тогда  S (трапеции) =S (ΔАВК) , т.к высоты этих фигур равны .

Пусть ВН⊥АD,  АН=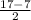   = 5 . Из ΔАВН , по т. Пифагора

ВН=√(13²-5²)=  √( (13+5)(13-5))=√(18*8)=12 .

S (трапеции)=1/2*12*(17+7)=144 (ед²).

4) ΔАВН-прямоугольный, tg∠BAD=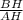  , tg∠BAD=  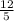, tg∠BAD=2,4 .

5) cos∠BCD= cos∠ABC, тк углы при основании равны.

cos∠ABC=cos(90°+∠АВН) =( по формулам приведения)=- sin∠ABН

Из ΔАВН,  sin∠ABН =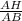  , sin∠ABН = 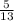 . Получаем  cos∠BCD=-  .

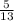6) ΔАВС , по т. косинусов АС²=АВ²+ВС²-2*АВ*ВС*cos∠ABC,

AC²=169+49-2*13*7*( -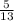  ) , AC²=218+70 ,  AC²=288 , AC=12√2.

7) Из формулы S=1/2*P*r , r=(2*S)/P . r=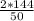  ,  r =5,76

8) Радиус описанной окружности для трапеции совпадает с радиусом описанной окружности для ΔАВС. Найдем R для ΔАВC по т. синусов

=2R ,   =2R .

sin∠ABC=sin(90+∠ABH)=( по формулам приведения) =сos∠ABH.

ΔABH , сos∠ABH=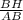  , сos∠ABH=  .Поэтому   sin∠ABC=  .

2R =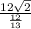   , R=6,5√2 .