решить решить
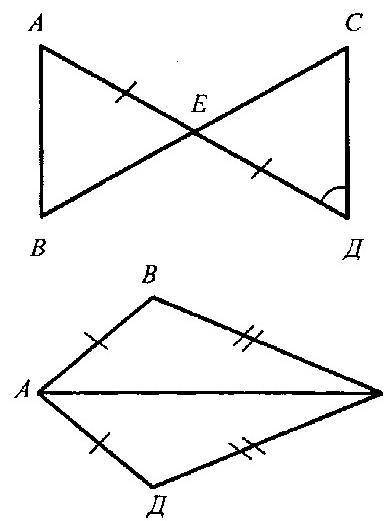
1) докажите равенство треугольников АВЕ и ДСЕ на рисунке 1, если АЕ=ЕД,<А=<Д. найдите стороны треугольника АВЕ, если ДЕ 3см, ДС 4см, ЕС 5см
2) на рисунке 2 АВ=АД, ВС=СД, докажите, что луч АС биссектриса угла ВАД
Ответы
Давайте приступим к решению задачи!
1) Нам нужно доказать равенство треугольников АВЕ и ДСЕ на рисунке 1, если АЕ=ЕД и <А= <Д.
Для начала, посмотрим на то, что дано: АЕ=ЕД и угол А равен углу Д.
Это означает, что у нас есть две равные стороны и равные углы. Это уже говорит о том, что у нас есть два равных треугольника.
Чтобы более точно доказать равенство треугольников, используем одну из аксиом геометрии - SSA (сторона-сторона-угол).
В нашем случае, мы знаем, что сторона АЕ равна стороне ЕД, сторона АВ общая для обоих треугольников, и угол А равен углу Д.
Теперь, рассмотрим стороны треугольника АВЕ. У нас есть сторона АЕ, которая равна 3 см, и сторона АВ, которая неизвестна.
Мы можем найти сторону АВ, используя теорему косинусов. Теорема косинусов гласит: c^2 = a^2 + b^2 - 2abcosC, где c - сторона напротив угла C.
В нашем случае, сторона АВ - сторона, которую мы ищем, сторона АЕ - известная сторона, равная 3 см, и угол, напротив которого стоит сторона АЕ, у нас тоже известен, потому что угол А равен углу Д, и ДЕ - известная сторона, равная 3 см.
Подставим известные значения в формулу и найдем сторону АВ:
АВ^2 = 3^2 + 3^2 - 2 * 3 * 3 * cos(<А)
АВ^2 = 18 - 18 * cos(<А)
Теперь, чтобы узнать значение стороны АВ, нам нужно знать значение угла А. В вопросе у нас не указано конкретное значение угла А, поэтому мы не можем найти точное значение стороны АВ. Однако, мы можем найти выражение для стороны АВ, используя значение угла А.
Таким образом, мы можем сказать, что сторона АВ = √(18 - 18 * cos(<А)).
Поэтому, чтобы доказать равенство треугольников АВЕ и ДСЕ, мы можем сказать, что сторона АВ = √(18 - 18 * cos(<А)), сторона ЕС = 5 см (дано), а сторона ДС = 4 см (дано).
2) Нам нужно доказать, что луч АС является биссектрисой угла ВАД на рисунке 2, при условии, что АВ=АД и ВС=СД.
Рассмотрим данные: АВ=АД и ВС=СД.
Это означает, что у нас есть две равные стороны. Если мы также докажем, что угол АСВ равен углу САД, то это будет говорить о том, что луч АС является биссектрисой угла ВАД.
Мы знаем, что АВ=АД и ВС=СД. Это значит, что у нас есть две равные стороны. Если мы докажем равенство углов АСВ и САД, то это будет говорить о том, что угол АСВ равен углу САД.
Для того чтобы доказать равенство углов, можно использовать аксиому "равные хорды равных окружностей образуют равные дуги".
В нашем случае, мы можем сказать, что у нас есть две окружности с центрами в точках B и D, радиусом, равным половине АВ, и они пересекаются в точке С.
Таким образом, по аксиоме "равные хорды равных окружностей образуют равные дуги", у нас есть равные дуги по обе стороны от АС. Это значит, что угол АСВ равен углу САД.
Таким образом, мы доказали, что луч АС является биссектрисой угла ВАД.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Популярные вопросы
- Рассчитать какую массу и какой объем займут 3 моль H2S?...
1 - Почему я не могу зайти на аккаунт в знания.ком? Но если захожу на свой во то...
2 - Тавро Кассандры -Почему роман так называется? -Что вы можете сказать о жанре...
3 - 2,6 ; 4,3 ; 5,1= 3,4 ; 3,8 ; 4,4 ; 4,9 ; 5,2=...
3 - 1.Признаком противоправного поведения является: 1) нарушение моральных норм...
3 - СА – шеңберге жанама. ∠ВАС бұрышының градустық шамасын табыңыз....
1 - Розвязати ріняння x2+12x=0...
2 - Определите количество протонов, нейтронов и электронов в 32S Количество протонов...
2 - У Сергея есть пять футболок и шесть пар сапогов. Сколько вариантов выбрать...
2 - На подворе 9 уток,а кур в 3 раза больше. На сколько больше кур чем уток? Краткая...
2