РЕШИТЬ ПОШАГОВО ,С РИСУНКОМ диагональ прямоугольного параллелепипеда с плоскостью основания образует угол 60 градусов , длины оснований 5 см и 12 см.
Вычисли высоту ..........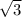 см

Привет! Я буду рад помочь тебе с решением этой задачи. Давайте разберемся пошагово.

Первым шагом нам необходимо найти длину диагонали прямоугольного параллелепипеда с плоскостью основания, которая образует угол 60 градусов. Мы можем использовать теорему Пифагора для решения этой задачи.

Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы (наибольшей стороны треугольника) равен сумме квадратов длин двух других сторон.

В данном случае, одна сторона треугольника - это длина основания прямоугольного параллелепипеда, равная 5 см, а другая сторона - это длина другого основания, равная 12 см. Давайте назовем диагональ треугольника "d" и высоту треугольника "h".

Мы знаем, что угол между диагональю и длиной основания равен 60 градусов. Используя геометрический закон, мы можем увидеть, что полученный треугольник является прямоугольным треугольником. А теперь, применим теорему Пифагора:

d² = 5² + 12²

Решим это уравнение:

d² = 25 + 144

d² = 169

Теперь возьмем квадратный корень из обеих сторон:

d = √169

d = 13

Таким образом, длина диагонали прямоугольного параллелепипеда с плоскостью основания равна 13 см.

Теперь перейдем ко второй части задачи - нахождению высоты параллелепипеда. Мы знаем, что высота образует прямой угол с плоскостью основания и диагональю. Помните, что в прямоугольном треугольнике с углом 90 градусов (прямым углом), гипотенуза (в нашем случае - диагональ) равна геометрическому среднему арифметических длин катетов (в нашем случае - длин оснований).

Поэтому мы можем записать:

d = √(h² + (5/2)² + (12/2)²)

Теперь подставим значение диагонали, которое мы нашли ранее:

13 = √(h² + (5/2)² + (12/2)²)

Теперь возводим обе стороны уравнения в квадрат:

13² = h² + (5/2)² + (12/2)²

169 = h² + (25/4) + (36/4)

Теперь приводим к общему знаменателю и складываем дроби:

169 = h² + (61/4)

Переносим (61/4) на другую сторону:

169 - (61/4) = h²

Упрощаем:

676/4 - 61/4 = h²

615/4 = h²

Теперь избавимся от квадрата, возведя обе стороны в квадратный корень:

√(615/4) = h

Находим корень:

√615/2 = h

Итого, высота прямоугольного параллелепипеда с плоскостью основания составляет (ответ округляем до двух десятичных знаков):

h ≈ 7.85 см

Надеюсь, мой ответ был понятным и помог разобраться в этой задаче. Если у тебя есть еще вопросы, не стесняйся задавать!"