решить подобные треугольник
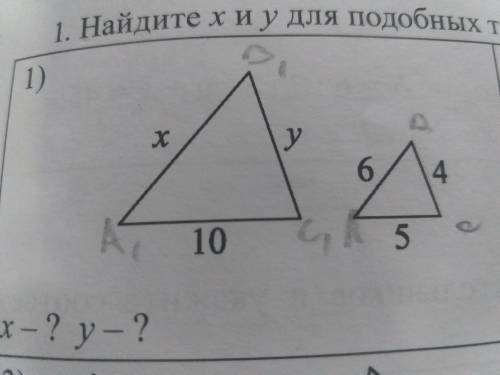
Другие вопросы по теме Геометрия
Популярные вопросы
- Окружающий мир: составь схему цепи питания, характерной для пустыни. в заранее...
3 - Кдуховной культуре не относятся: 1)религиозные учения 2)анегдоты о политиках...
2 - развития дыхательной системы...
3 - 1)в каком случае вес тела по модулю равен силе тяжести 2)как изменяется...
2 - Вкаких случаях и зачем ставиться в языке артикль a ?...
2 - Придумайте концовку к произведению дубровский а.с.пушкина. известно что...
3 - Решите уравнения 1/5(x+4)=3 1/4(2y+1)=8 -1/7(5u-7)=6...
3 - Составьте фразы позволяющие вежливо отказаться от покупки. 30 заранее...
2 - Что свидетельствовало о начале распада первобытнообщинного строя?...
1 - Вдвух коробках по 10 вафель. марина съела несколько вафель из первой коробке.лариса...
2
x=12 y=8 ВРОДЕ
Объяснение:
х=12,у=8
кажется так
Для начала, давайте вспомним, что такое подобные фигуры. Две фигуры называются подобными, если их соответствующие углы равны, а соответствующие стороны пропорциональны.
По условию, у нас есть два треугольника — большой и маленький. Давайте обозначим их стороны:
1. В большом треугольнике:
- Длина горизонтальной стороны (основание) равна 12см.
- Длина вертикальной стороны составляет 8см.
2. В маленьком треугольнике:
- Длина горизонтальной стороны (основание) равна x.
- Длина вертикальной стороны составляет 4см.
Теперь мы можем приступить к проверке подобия треугольников. Для этого необходимо сравнить соответствующие углы.
Большой треугольник имеет прямой угол между горизонтальной и вертикальной сторонами. Маленький треугольник также имеет прямой угол между его горизонтальной и вертикальной сторонами. Следовательно, соответствующие углы в обоих треугольниках равны.
Теперь давайте проверим, являются ли соотношения сторон треугольников пропорциональными. Мы можем использовать соотношение длин сторон горизонтальной и вертикальной сторон треугольников:
Для большого треугольника:
- Горизонтальная/вертикальная = 12/8
Для маленького треугольника:
- Горизонтальная/вертикальная = x/4
Чтобы проверить, являются ли эти соотношения равными, мы можем сократить их до наименьших значений:
Большой треугольник:
- 12/8 = 3/2
Маленький треугольник:
- x/4
Теперь мы можем установить равенство этих двух соотношений и решить уравнение:
3/2 = x/4
Мы можем преобразовать это уравнение, чтобы избавиться от дробей:
3 * 4 = 2 * x
12 = 2x
Теперь мы можем найти значение x, разделив обе стороны уравнения на 2:
12/2 = x
6 = x
Таким образом, длина горизонтальной стороны (основания) маленького треугольника составляет 6см.
Получается, что соотношение между длинами сторон большого треугольника и маленького треугольника равно 12/8 = 3/2, или 6/4 = 3/2. Эти соотношения пропорциональны, что означает, что треугольники являются подобными. Значение x, равное 6, указывает на длину горизонтальной стороны (основания) маленького треугольника.