решить Отношение меньшего основания трапеции к средней линии 3:5.В каком отношении делит диагональ этой трапеции ее площадь.

Ответы

армен459 15.10.2020 15:58

7:3

Решение задания прилагаю

ПОКАЗАТЬ ОТВЕТЫ

асаса3 15.10.2020 15:58

Пусть a - меньшее основание, b - большее основание, m - средняя линия. Тогда по условию:

$\frac{a}{m} = \frac{3}{5} = \frac{2a}{a+b} = \frac{3}{5} = 10a = 3a+3b = 7a = 3b = b = \frac{7}{3}a$

Теперь рассмотрим ΔABC. Его площадь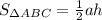 $S_{\Delta ABC} = \frac{1}{2} ah$ , где h - это высота трапеции. Аналогично для ΔACD: $S_{\Delta ACD} = \frac{1}{2}bh$ .

Тогда отношение площадей равно:

$\frac{S_{\Delta ABC}}{S_{\Delta ACD}} = \frac{\frac{1}{2}ah }{\frac{1}{2}bh } = \frac{a}{b} = \frac{a}{\frac{7}{3}a } = \frac{3}{7}$

ответ: $\frac{3}{7}$

решить Отношение меньшего основания трапеции к средней линии 3:5.В каком отношении делит диагональ э

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

castlecrashers 20.05.2020 10:35

Точка дотику кола вписаного в рівнобічну трапецію ділить її бічну сторону на відрізки 9 см і 4 см. Знайдіть площу трапеції....

СвятойТапочек 20.05.2020 10:35

быстро нужно желательно с чертежами...

UlianaModerator 20.05.2020 10:35

Відстань від вершини А1 куба ABCDA1B1C1D1 до прямої BD дорівнює 18 см. Знайдіть відстань між прямими BD і A1C....

irnairina89 20.05.2020 10:35

У рівнобедреного трикутнику FKC з основою FC...

iwliliya18 20.05.2020 10:34

Лёгкие !! Найдите тангенс угла по рисунку!...

пупсикг 17.06.2019 07:10

Втрапеции нижнее основание равно 6 см, а средняя линия в 1.5 раза больше верхнего основания.найдите верхнее основание....

ddaler 17.06.2019 07:10

Отрезки am и bn пересекаются в точке c. известно,что ab=bc и cn=mn. найдите величину угла abc,если угол cnm=58...

DashaCat02 17.06.2019 07:10

Втрапеции нижнее основание равно 6см, а средняя линия в 1.5 раза больше верхнего основания.найдите верхнее основание....

ТёмаТащер 17.06.2019 07:10

Площадь боковой поверхности цилиндра равна 60п м2 а радиус основания 5м найдите длину образующей цилиндра...

Marshmelloo 17.06.2019 07:10

Стороны параллелограмма равны 4м и 6м, а один из его углов в 2 раза меньше другого. найдите площадь параллелограмма и еще 1-а дано: треугольник авс,ас=квадратному корню из 2-ух...

решить Отношение меньшего основания трапеции к средней линии 3:5.В каком отношении делит диагональ этой трапеции ее площадь.

Популярные вопросы