решить номер 17.С полным оформлением. ​

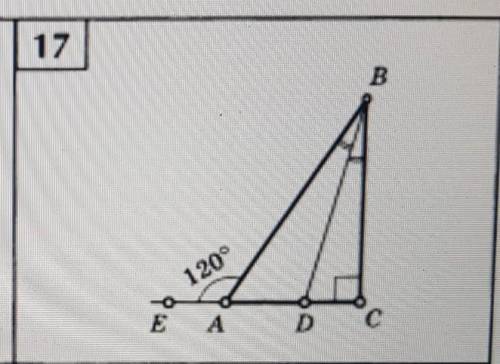
В прямоугольном ΔАВС, ∠С=90° , ВD-биссектриса , внешний угол ∠ВАЕ=120°. Найти углы ΔАВС.

Объяснение:

Дано : ΔАВС, ∠С=90° , ВD-биссектриса , внешний угол ∠ВАЕ=120°. Найти : ∠АВD, ∠DBC,∠ABC,∠BAC.

Решение . Внешний угол равен сумме двух внутренних , не смежных с ним : ∠ЕАС=∠АВС+∠С,

              120°=∠АВС+90°,   ∠АВС=30°.

ВD-биссектриса ⇒ ∠АВD = ∠DBC=30°:2=15°  .

∠ВАС=180°-120° =60° , по т. о смежных углах.

ответ. ∠АВD= 15° , ∠DBC=15° ,∠ABC=30° ,∠BAC=60°.