Решить их всех.
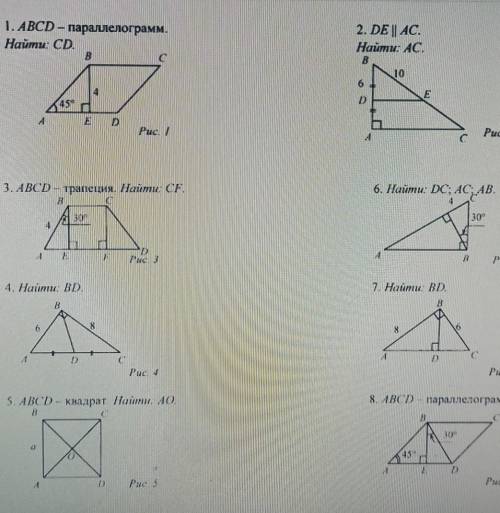
ABCD- Параллелограмм
найти cd
Другие вопросы по теме Геометрия
Популярные вопросы
- Составить таблицу «сравнительная характеристика Индии и Китая по плану» План: 1....
3 - Даны точки А(2;3;-1)и В(0;1;4).Найдите координаты вектора АВ: Даны точки А(2;3;-1)и...
2 - Русский язык Задание: Подготовить сообщение по творчеству М.Е.Салтыкова-Щедрина...
2 - Вычислите и запишите неизвестные углы...
1 - При рычага приподняли дверь весом 0,84 кН, действуя на длинное плечо силой 30Н....
2 - Cрочно График функции y= kx+b параллелен оси абсцисс и проходит через точку p=(...
3 - 2(х-5) -5=13-4х развязати рівняння Задача Площа Тихого океану вдвічі більша за площу...
2 - Какие ценности оказываются главными для Робинзона Крузо? Почему?...
2 - Даны точки А( 0, 2, 1) В(2, 1, 1) С(1, 1, 2). Вычислите угол между векторами СА...
3 - 1. Напишіть свої міркування про те, яких політичних помилок припустив Яким Сомко?...
3
Поскольку ABCD - параллелограмм, то стороны AB и CD параллельны и имеют одинаковую длину. В данном случае, изображеном на рисунке, длина стороны AB равна 8 см.
Теперь, чтобы найти длину отрезка CD, нам необходимо рассмотреть прямоугольный треугольник ADC. Зная длину стороны AB и угол при вершине D, мы можем найти длину стороны AD с помощью тригонометрии.
Для этого, мы можем использовать теорему синусов, которая говорит о следующем соотношении:
AD/sin(угол при вершине D) = AB/sin(угол при вершине A)
Используя данную формулу и известные нам значения, мы можем выразить длину стороны AD:
AD/sin(угол при вершине D) = 8/sin(60°)
Значение sin(60°) равно √3/2, поэтому:
AD/sin(угол при вершине D) = 8/(√3/2)
Теперь, чтобы найти длину отрезка CD, нам необходимо рассмотреть прямоугольный треугольник BCD. Мы уже знаем длину стороны AB (равную 8 см), а также длину стороны AD, которую мы только что нашли.
Поскольку стороны AB и CD параллельны и имеют одинаковую длину, то длина отрезка CD также равна 8 см.
Таким образом, мы можем заключить, что длина отрезка CD равна 8 см.