решить эту задачу по геометрии,даю 20б !

Ну : ОА - бисектриса ( делит пополам сичну ( по-моему )) 180:2 =90 . Дальше извиняй , не помню

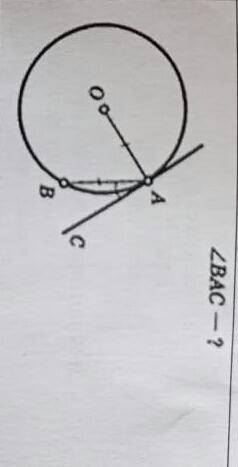
∠BAC = 30°

Объяснение:

Проведем отрезок OB и рассмотрим ΔAOB. Так как OA = OB как радиусы, а по условию OA = AB, то AO = AB = OB, тогда треугольник ΔAOB правильный, а по свойству правильного треугольника все его углы равны 60°. OA - касательная к окружности, тогда ∠OAC = 90°.

∠OAC = ∠OAB + ∠BAC ⇒ ∠BAC = ∠OAC - ∠OAB = 90° - 60° = 30°.