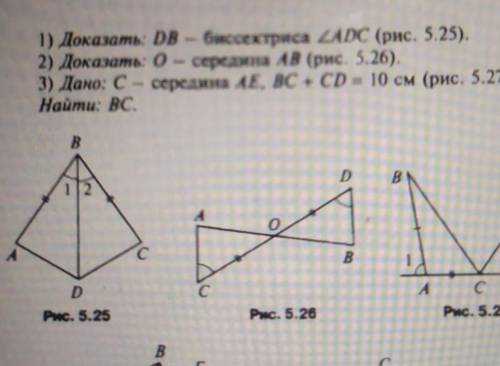
решить: доказать DB- биссектриса угла ADC. рисунок 5.25
Другие вопросы по теме Геометрия
Популярные вопросы
- с физикой, 7 класс! 1. Чем вызвано сохранение твердым телом...
1 - 2 бромо 3 3 дихлорогексан...
1 - Краткий конспект на тему АХОВ и их классификация умоляю не пишите...
2 - Не виконуючи побудови, визначте вид чотирикутника АВСD (паралелограм,...
1 - Напишите: да, нет и почему...
2 - Чему учит рассказ Шаповалова танюшкино солнышко...
1 - Верны ли суждения о социальных нормах...
3 - Разгадайте ребус чтобы узнать название литературного жанра....
3 - Прочитайте отрывок из повести И.С.Тургенева «Ася». Составьте...
1 - Вася нашёл числа, обратные к числам и , сложил их и нашёл обратное...
3
Определение биссектрисы угла гласит, что биссектриса угла делит его на два равных угла.
Для начала, давайте обратим внимание на треугольник ADC, в котором мы хотим доказать, что DB является биссектрисой угла ADC.
Мы видим, что у нас есть стороны AD и DC, а также угол ADC.
Для доказательства, что DB является биссектрисой угла ADC, мы должны доказать, что угол ADB и угол BDC равны между собой.
1. Обратимся к углу ADB.
Мы можем заметить, что стороны AD и DB являются общими для углов ADB и ADC.
Также, мы имеем вертикальные углы ADE и BDC, которые равны между собой, так как являются вертикальными углами.
2. Вспомним, что по определению биссектрисы угла, биссектриса угла делит его на два равных угла.
Это значит, что угол ADB и угол BDC должны быть равны между собой.
Таким образом, мы доказали, что DB является биссектрисой угла ADC.