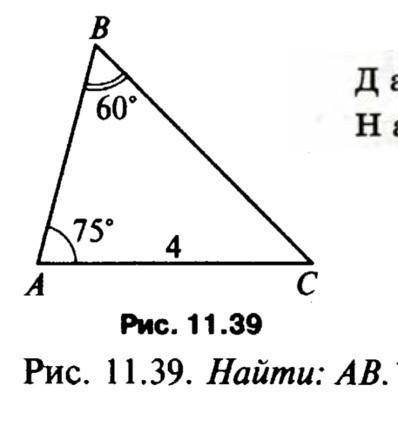
Решить через теорему синусов
Другие вопросы по теме Геометрия
Популярные вопросы
- У чому полягають особливості життедіяльності тварин порівняно з...
1 - Как переводится выражение Покляпая берёза в былинах...
3 - Напишите мини рассказ по типу мне понравилась эта книга потому что...
3 - 12 тапсырма. Кластер құра я вообще не шарю...
2 - Написать эссе по теме ,,Истоки российской модернизации в конце 17...
2 - решите все правильно в низу есть подсказка. география 7 класс...
3 - Книга, которую стоит прочитать в 10 классе. Нужно написать мини...
3 - Перепишіть, розтавляючи пропущені розділові знаки. однорідні члени...
2 - Коротке повідомлення про одного з українських учених-географів...
1 - Какие из лучей,изображённые на рис. 14,лежат на прямой AB? а какие...
3
Для начала, обозначим A, B и C вершины треугольника, а, b и c стороны, напротив соответствующих вершин.
Дано, что угол A равен 55 градусам (A = 55°), а сторона b имеет длину 11 (b = 11).
Атеперь, чтобы найти значение стороны c, мы можем использовать следующую формулу теоремы синусов:
a/sin(A) = c/sin(C)
В нашем случае, a - это сторона, напротив угла C, которую мы не знаем, но можем найти. Сделаем замену:
a = c * sin(A) / sin(C)
Теперь нам нужно найти значения стороны a и угла С. Для нахождения угла С, можно использовать сумму углов треугольника:
C = 180° - A - B
C = 180° - 55° - 75°
C = 50°
Теперь мы можем найти значение стороны a:
a = c * sin(A) / sin(C)
a = c * sin(55°) / sin(50°)
После нахождения значения стороны a, мы можем найти значение стороны c, используя изначальную формулу теоремы синусов:
a/sin(A) = c/sin(C)
c = a * sin(C) / sin(A)
Теперь мы можем подставить известные значения в формулу:
c = a * sin(50°) / sin(55°)
Подставим значение стороны a:
c = (c * sin(55°) / sin(50°)) * sin(50°) / sin(55°)
Заметим, что sin(50°) / sin(55°) сокращаются, поэтому получаем:
c = c
Таким образом, длина стороны c равна значение стороны b и составляет 11.
Подытожим:
Длина стороны c, напротив угла C, равна 11. В равномерно тупоугольном треугольнике сторона, напротив угла C, всегда равна длине другой известной стороны treugolnika.
Надеюсь, это решение понятно. Если у вас возникли дополнительные вопросы, не стесняйтесь задавать.