решить ............................

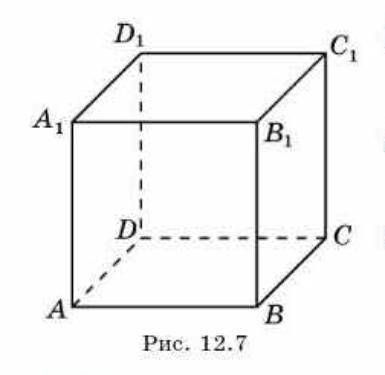
Расстояние от точки до плоскости равно длине перпендикуляра из этой точки на плоскость.

Этот перпендикуляр будет лежать в плоскости ВДД1В1.

Получаем прямоугольный треугольник ВОВ1.

Перпендикуляр ВЕ к ОВ1 и есть искомый.

ОВ = √2/2 как половина диагонали квадрата основания.

ОВ1 = √((√2/2)² + 1²) = √(3/2).

ВЕ = 2S/OB1 = (2*(1/2)*(√2/2)*1)/√(3/2) = 1/√3 = √3/3.

=================================

Объяснение: