решить ..................................

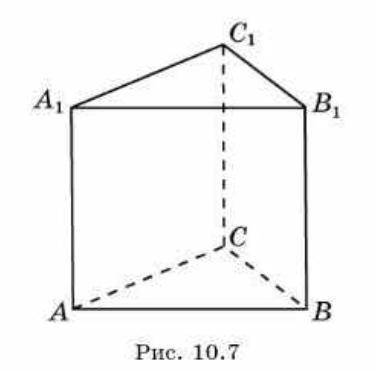
АС₁=АВ₁ - как диагонали равных квадратов.

Тогда в равнобедренном треугольнике АС₁В₁ надо найти высоту, проведенную к С₁В₁, это и будет искомое расстояние. АВ₁=√(АВ²+ВВ₁²)=√(1+1)=√2, Высота в треугольнике АС₁В₁ может быть найдена по теореме Пифагора. Пусть О- середина С₁В₁, и т.к. высота  АО, проведенная к стороне С₁В₁ совпадает с медианой, нам остается посчитать длину медианы в ΔАС₁В₁; АО= √(АВ₁²-ОВ²)=√(2-(1/4))=√7/2