Ребро DA тетраэдра DABC перпендикулярно плоскости АВС. АВ=ВС=АС=8см,ВД=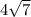
. Найдите двугранный угол грани которого содержат треугольники АВС и ВСД
​

Для начала, давайте проведем несколько вспомогательных шагов, чтобы лучше понять данную задачу.

1. Построим тетраэдр DABC.

C
/|\
/ | \
/ | \
B–––|–––A
\ | /
\ | /
\|/
D

В данном тетраэдре, у нас есть точка D, которая находится на ребре DA. Она просто указывает на то, что ребро DA - высота тэтраэдра DABC.


2. Проведем высоту ВД и обозначим точку пересечения высоты и плоскости ABC как точку H.

C
/|\
/ | \
/ | \
/ H \
B–––|–––A
\ | /
\ | /
\|/
D

Точка H является основанием высоты ВД. Она является пересечением плоскости ABC и ребра ВД.


3. Очевидно, что треугольник DHC является равнобедренным, так как ВС=АС и ВД=ДС. Также, так как высоты перпендикулярны к основаниям, то они являются высотами треугольников DAB и DBC.

Зная все это, мы можем в дальнейшем использовать данные свойства, чтобы решить эту задачу.

Теперь, проведем более детальные шаги решения задачи:

1. Найдем высоту треугольника АВС, используя теорему Пифагора.
Выразим длину высоты АН в треугольнике АВС:
АН² = АВ² - ВН²
(где АВ=ВС=АС=8см)
АН² = 8² - (4√7)²
АН² = 64 - 16 * 7
АН² = 64 - 112
АН² = -48

Так как АН² получилось отрицательным, это означает, что треугольник АВС является остроугольным и высота перпендикулярна основанию ВС.


2. Так как мы знаем, что высота ВД равна √7, то это значит, что треугольник DBC - прямоугольный.

У нас есть все данные для нахождения двугранного угла грани, который содержит треугольники АВС и ВСД. Мы можем использовать тангенс угла.

3. Найдем двугранный угол грани, используя тангенс угла.

tan(∠BDC) = (противолежащий катет) / (прилежащий катет)
= ВД / ВС
= √7 / 8

∠BDC = arctan(√7 / 8)

Можете использовать калькулятор, чтобы получить численное значение угла.

Примечание: Если вам нужно выразить угол в радианах, просто умножьте численное значение на π / 180.

Это и есть подробное и обстоятельное решение задачи. Надеюсь, что оно оказалось понятным для вас.