РАЗОБРАТЬСЯ
Прямая l касается окружности с диаметром AB в точке C; M и N — проекции точек A и B на прямую l, D — проекция точки C на AB. Докажите, что CD2 = AM . BN.

Другие вопросы по теме Геометрия
Популярные вопросы
- Дано ,ACB Угод C =90° Ab=6 см УголA=39° Знайти: BC,AC,iугол B....
1 - Сиетезированный полимер представлен следующими аминок-тами: Аланин, глутамин,...
1 - Аналіз вірша моя кохана пишна рожа...
1 - Строительство пирамиды Хеопса. Используя знания по истории, расскажите об этом...
1 - Решите номер 4 и 5 и6 6 класс...
2 - Ежелгі Мысырда, Үндістанда, Грекияда (жөндеушілер,жұлдызшылар, оқушылар) болған....
2 - Отрезок АД является биссектрисой треугольника АВС. найти вд и дс если ав =14см,...
2 - Вычислите объем газа, который образуется при взаимодействии раствора массой...
1 - Высшая математика, матрицы, найдите значение Х....
2 - Знайдіть активність зразка, у якому міститься 101° ядер Плутонію-239. Стала...
3
Решение : ///////////////////////////////////
Доказательство:
1) См. рисунок 1
∠AMC = 90° т.к M - проекция A на l
∠)OCN = 90° т.к l - касательная к окружности в точке C, OC - радиус в точку касания
Следовательно AM || OC
Значит ∠MAC = ∠ACO
AO = OC (как радиусы) ⇒ ΔACO - равнобедренный ⇒ ∠CAO = ∠ACO
Значит ∠MAC = ∠CAO
∠MCA = 90 - a
∠DCA = 90 - a (∠CDA = 90° т.к D - проекция C на AB)
Следовательно ∠MCA = ∠DCA
Откуда следует, что ΔMAC = ΔDAC по стороне и двум углам (AC - общая)
А значит AM = AD
2) Аналогично доказывается BD = BN (см. Рисунок 2)
3) См. Рисунок 3.
∠ACB = 90° т.к опирается на диаметр
В ΔABC: ∠CAB = 90° - ∠CBD
В ΔCBD: ∠DCB = 90° - ∠CBD
Следовательно ∠CAB = ∠DCB
Откуда следует, что ΔABC подобен ΔCBD по двум углам.
Значит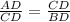 ⇒
⇒ 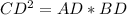
Из пунктов 1 и 2:
AM = AD
BD = BN
Следовательно
Доказано
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!