РАЗОБРАТЬСЯ

Две медианы треугольника перпендикулярны. Найдите отношение третьей его медианы к соответствующий стороне.​

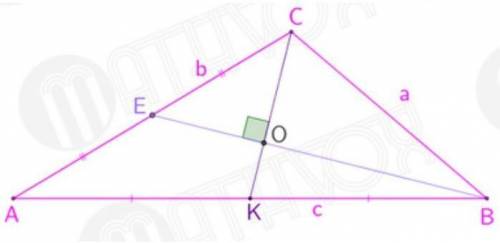
1) Проведем медиану AP, ⇒ CP = PB.

2) AO:OP = 2:1 (по свойству пересекаемых медиан)

3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)

4) OP — медиана ΔCOB, т.к.  ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.

Следовательно, OP = 1/2CB, или OP:CB = 1:2

5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.

ответ: отношение третьей медианы к соответствующий стороне — 3:2.