РАЗОБРАТЬСЯ

Через произвольную точку P
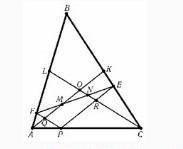
стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.​

Через произвольную точку P  стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.​

Объяснение:

1) Медианы треугольника точкой пересечения делятся 2:1 , считая от вершины:  ОК=1/3*АК  ; LO=1/3*LC.

2)РЕ║АК  ⇒  RE=1/3*PE,

   PF║CL  ⇒   QF=1/3*PE.

3)ΔREN подобен ΔPEF ( по 2 углам, там целая куча соответственных   углов), значит сходственные стороны пропорциональны⇒

EN/EF=RE/PE  или EN/EF=1/3 или EN=1/3*EF ;

  ΔQFM подобен ΔPFE( по 2 углам) ,значит сходственные стороны пропорциональны⇒ FM/EF=QF/PE  или FM/EF=1/3 или FM=1/3*EF.

4) Получили , что  M и N разделили отрезок FE на 3 равные части.