Расстояние между центрами окружностей радиусов 2 и 1 равно . найдите площади образовавшихся луночек и общей части кругов.
Ответы
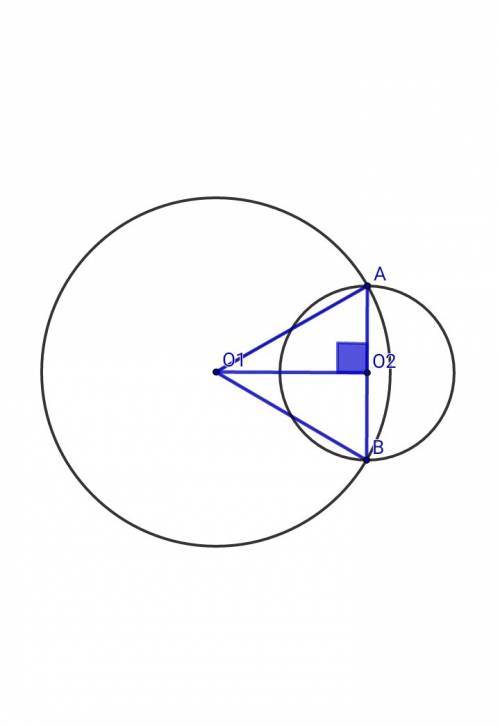
AO₁ = 2 , AO₂ = 1 , O₁O₂ = √3Для ΔАО₁О₂ выполняется теорема Пифагора: АО₁² = О₁О₂² + АО₂² ; 2² = (√3)² + 1² ; 4 = 4 ⇒ ΔАO₁O₂ - прямоугольный, O₁O₂⊥ABΔАО₁В - равнобедренный, АО₁ = BO₁ = 2 ⇒ O₁O₂⊥AB, AO₂ = BO₂ = 1AO₁ = BO₁ = AB = 2 ⇒ ΔAO₁B - равностороннийПлощадь круга с радиусом R₁ = 2: S₁ = πR₁² = 4πПлoшадь круга с радиусом R₂ = 1: S = π S ao₁b = AB²√3/4 = 4√3/4 = √3Площадь ме'ньшего сектора, соединяющего точки А, О₁, В:S сек. = πR₁²•α/360° = π•R₁²•∠AO₁B/360° = 4π•60°/360° = 2π/3S ceк. = S ao₁b + SS = S сек. - S ao₁b = (2π/3) - √3Площадь общей части кругов: S₃ = (S₂/2) + S = (π/2) + (2π/3) - √3 = (7π/6) - √3Площадь бо'льшей луночки: S₄ = S₁ - S₃ = 4π - ( (7π/6) - √3 ) = 4π - (7π/6) + √3 = (17π/6) + √3Площадь ме'ньшей луночки: S₅ = (S₂/2) - S = (π/2) - ( (2π/3) - √3 ) = (π/2) - (2π/3) + √3 = √3 - (π/6)
ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия
Популярные вопросы
- Выберите два числа,сумма которых равна 72,а частное 2! 36и36,48и24,60и12,66и6....
1 - Рассказать о быте,традициях,обычаях османской империи! ! ...
3 - Сочинение на тему рябина в моём селе...
1 - Дана равнобедренная описанная трапеция abcd с основаниями ad=16 и bc=12....
1 - Dano: fk a me=dmd = de ; pd = dkdok-mbi lr md=l dep-r...
1 - Алтын сойко деген созго суйлом тузуп бергилечи...
1 - Что не делают паразитные шестеренки?...
1 - Рассказ о кувандыкского района...
3 - Вчем заключалась внутренняя политика консульства и наполеоновской империи...
2 - Устинов и иванов, 15 и 17 лет, шли по улице, подталкивая друг друга, бросались...
1