1. Геометрия
  2. Радиус основания конуса равен

Радиус основания конуса равен 6,а высота конуса 8.в конусе проведено сечение плоскостью,проходящей через вершину конуса.площадь сечения равна найдите угол между плоскостью основания и плоскостью сечения. ответ должен получиться пишите,, подробное решение .

doc2934 doc2934    2   22.05.2019 09:00    0

Ответы
3333231231 3333231231  01.10.2020 06:32

Исходя из рисунка 3 в приложении, площадь сечения равна:

S=\frac12ab*sin\alpha

sin\alpha=\frac{2S}{ab}=\frac{2*25\sqrt3}{10*10}=\frac{\sqrt3}{2}

\alpha=60^o

Т.к в сечении треугольник равнобедренный, получаем:

\alpha=180-\beta+\gamma=180-2\beta=180-2\gamma

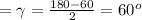
Откуда: \betta=\gamma=\frac{180-60}{2}=60^o

Т.е этот треугольник правильный, тогда высота сечения будет равна:

h_c=sin60*10=5\sqrt3

Тогда получаем искомый угол будет равен:

sina=\frac{h}{h_c}

sina=\frac{8}{5\sqrt3}

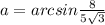
a=arcsin\frac{8}{5\sqrt3}

ответ:a=arcsin\frac{8}{5\sqrt3}

 

P.S Указанный вами ответ, возможно неверно переписан, т.к ответ полученный в данной задаче, найден обоснованно


Радиус основания конуса равен 6,а высота конуса 8.в конусе проведено сечение плоскостью,проходящей ч
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
dashashubina55 dashashubina55  07.05.2020 11:43
Высота правильной четырехугольной пирамиды равна 6см, а площадь основания 4 см. Найти боковое ребро....
sonka1001p0arxp sonka1001p0arxp  07.05.2020 11:43
В прямоугольную трапецию ABCD вписана окружность, АВ перпендикулярна AD. Угол В равен 30 градусов, ВС = 8 см. Найдите периметр трапеции....
Larisa150301 Larisa150301  07.05.2020 11:43
Дан прямоугольный треугольник . Определи ∡ , если ∡ = 74°. Рисунок ниже ∡ = °....
Локи30 Локи30  07.05.2020 11:43
У рівнобедреному трикутнику підстава в 4 рази менше бічної сторони, а периметр дорівнює 61,2 см. знайти бічну сторону трикутника. Будь добрий до будь ласка....
mvrlin mvrlin  07.05.2020 11:43
Оберіть правильний варіант теореми синусів. 1 Сторони трикутника дорівнюють синусам протилежних до них кутів 2 Сторони трикутника обернено пропорційні синусам протилежних до них кутів...
botikalmas botikalmas  07.05.2020 11:42
Решить задачи:1. В треугольнике АВС АВ=ВС, АД-биссектриса, ∠АДВ= 120. Найти ∠А, ∠В,∠С2. В треугольнике СДЕ, ∠Д=90, СЕ+СД=31см, СЕ-СД=3см. Найти СД?Решить уравнением с одной переменной...
22a03a1989 22a03a1989  25.06.2019 06:50
Втреугольнике abc сторона аb равна 17 см, сторона ас равна 15 см, сторона вс равна 8 см. найдите наименьшую высоту этого треугольника....
шота1 шота1  25.06.2019 06:50
Катеты ст и сн прямоугольного треугольника тсн соответственно равны 15 дм и 20 дм. найдите высоту этого треугольника опущенную на гиппотенузу...
152003152003 152003152003  25.06.2019 06:50
Докажите, что четырехугольник a b c d является прямоугольником a (1; 2) b (2; 1) c (-1; -2) d (-2; -1)...
Xalk22 Xalk22  25.06.2019 06:50
Решите, ) диагональ куба равна 6 см. найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней....

Популярные вопросы