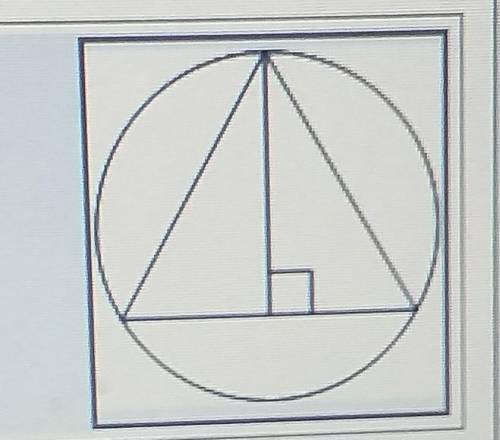
Радиус окружности, описанной около равностороннего треугольника, равен 16. Найдите высоту этого треугольника.​

Объяснение:

Смотри фото

Добрый день! Рад, что вы обратились ко мне за помощью. Давайте решим эту задачу вместе.

У нас имеется равносторонний треугольник, в котором каждая сторона равна другой и все углы равны 60 градусов. По условию, радиус окружности, описанной вокруг этого треугольника, равен 16.

Чтобы найти высоту треугольника, нам понадобится использовать свойство равносторонних треугольников, которое гласит: высота равностороннего треугольника является биссектрисой его угла и также является медианой и высотой.

Теперь давайте пошагово решим задачу.

Шаг 1: Найдем длину стороны треугольника.
Так как это равносторонний треугольник, все его стороны равны. Пусть длина каждой стороны равна a. Тогда, по свойствам равносторонних треугольников, мы можем записать уравнение:
a + a + a = 3a, где 3a - это периметр треугольника.
Так как все стороны треугольника равны, мы можем записать a = 3a / 3 или a = p / 3, где p - периметр треугольника.
Теперь нам нужно найти значение периметра треугольника. Мы знаем, что периметр треугольника равен 3p, где p - длина стороны треугольника. Подставим значение, которое мы нашли ранее:
3p = 3 * (p / 3) = p
Таким образом, мы получаем, что периметр треугольника равен p.

Шаг 2: Найдем длину окружности.
Мы знаем, что радиус окружности равен 16. Формула для вычисления длины окружности - это 2 * pi * r, где r - радиус окружности и pi - число пи, приблизительно равное 3.14159.
Подставим значение радиуса и решим уравнение:
2 * pi * 16 = 32 * pi.

Шаг 3: Связь длины стороны треугольника и длины окружности.
Мы знаем, что длина окружности равна периметру треугольника. Поэтому, мы можем записать уравнение:
32 * pi = p.

Шаг 4: Найдем длину стороны треугольника.
Так как мы имеем равносторонний треугольник, то длина каждой стороны равна p / 3 (как мы нашли на шаге 1). Подставим значение периметра из уравнения в шаге 3:
p = 32 * pi.
Значит, длина каждой стороны треугольника равна (32 * pi) / 3.

Шаг 5: Найдем высоту треугольника.
Мы знаем, что высота равностороннего треугольника является биссектрисой его угла. По условию, угол треугольника равен 60 градусов.
Согласно свойству биссектрисы, она делит угол на две равные части. Значит, у нас получится прямоугольный треугольник с гипотенузой p / 3 (длина стороны треугольника) и углом 30 градусов.
Теперь мы можем найти длину половины высоты треугольника, используя тригонометрическую функцию синуса (sin):
sin(30) = (противолежащий катет) / (гипотенуза).
sin(30) = (половина высоты) / [(p / 3)].
Раскрываем sin(30), зная, что sin(30) = 1/2:
1/2 = (половина высоты) / [(p / 3)].
Мы хотим найти половину высоты, поэтому умножим обе стороны уравнения на 2:
2 * (1/2) = (половина высоты) * (2 / (p / 3)).
Подставим значение периметра p, которое мы нашли на шаге 4:
1 = (половина высоты) * (2 / ((32 * pi) / 3)).
Упростим выражение:
1 = (половина высоты) * (6 / (32 * pi)).
Теперь умножим обе стороны уравнения на (32 * pi) / 6:
(32 * pi) / 6 = (половина высоты).
Упростим:
16 * pi / 3 = (половина высоты).
Теперь умножим обе стороны уравнения на 2:
32 * pi / 3 = высота треугольника.
Таким образом, мы нашли, что высота равностороннего треугольника равна 32 * pi / 3.


Вот и все! Мы получили ответ, что высота равностороннего треугольника равна 32 * pi / 3.