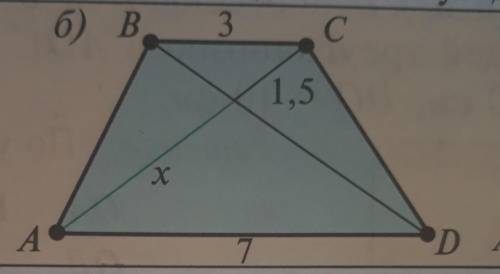
Пусть АВСД-трапеция.Найдите х используя данные рис,6​

3,5

Объяснение:

ВС/АД=СО/АО=> АО=АД×СО/ВС

АО=7×1,5/3=3,5

Дано:

ADCD - трапеция

ВС = 3

AD = 7

Диагонали АС и BD пересекаются в точке О.

СО = 1,5

Найти:

АО = х

ΔAOD  и ΔВОС подобны по двум углам (∠ВОС = ∠AOD как вертикальные; ∠ВСО = ∠DAO - накрест лежащие при ВС || AD и секущей АС)

В подобных треугольниках соответственные стороны пропорциональны

AD : BC = AO : CO

AO = AD · CO : BC

AO = 7 · 1.5 : 3

AO = 3.5

х = 3,5