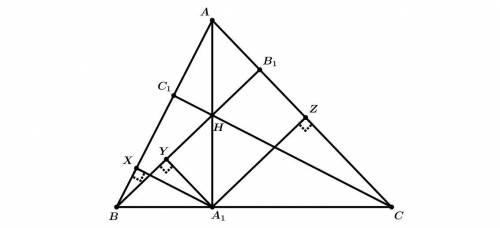
Пусть AA1, BB1, CC1 — высоты остроугольного треугольника ABC, пересекающиеся в точке H. Точки X, Y, Z — основания перпендикуляров из точки A1 на прямые AB, BB1, AC соответственно. Выберите 4 точки: 3 вершины треугольника и точку, лежащую на описанной окружности этого треугольника, такие, что на картинке есть 3 точки, лежащие на прямой Симсона выбранной точки относительно выбранного треугольника.

A

B

C

A1

B1

C1

X

Y

Z

H

likunya    3   10.04.2021 23:06    14