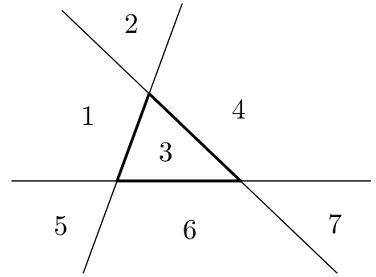
Прямые, содержащие стороны треугольника, разбивают плоскость на семь областей. В каких областях может находиться точка, изогонально сопряжённая точке из области 1?

Хорошо, давайте разберем этот вопрос по шагам.

1. Для начала, давайте определим, что такое точка, изогонально сопряженная точке из области 1.

Точка, изогонально сопряженная точке A, обозначается A' и определяется следующим образом: если провести лучи AB и A'B', где B - любая точка вокруг A, то эти лучи будут образовывать один и тот же угол. Таким образом, точка A' - это точка, из которой лучи, соединяющие ее с точками треугольника, образуют изогональные углы.

2. Теперь перейдем к рассмотрению областей, на которые разбивается плоскость.

Мы имеем треугольник ABC и три его стороны: AB, BC и AC. Каждая из этих сторон является прямой, которая разбивает плоскость на несколько областей.

3. Теперь найдем точку, изогонально сопряженную точке из области 1.

Для этого проведем лучи, соединяющие точку из области 1 с точками треугольника. Затем найдем точку пересечения этих лучей и обозначим ее A'.

4. Наконец, определим в каких областях может находиться точка A'.

Первоначально, на плоскости было разбито на семь областей. В результате проведения лучей из точки из области 1 и построения точки A', плоскость также была разбита на несколько новых областей.

Теперь найдем области, в которых может находиться точка A'. Мы увидим, что A' может находиться в областях 2, 3, 4, 5, 6 и 7.

Область 1 не может содержать точку A', потому что она расположена со стороны, противоположной треугольнику и не соединена с ним ни одним углом.

Таким образом, точка A' может находиться в областях 2, 3, 4, 5, 6 и 7.

Надеюсь, это пояснение помогло вам понять, в каких областях может находиться точка, изогонально сопряженная точке из области 1. Если у вас есть еще вопросы, не стесняйтесь задавать их.