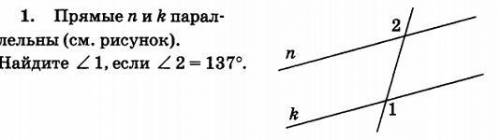
прямые n и k параллельны найдите угол 1 если угол 2 равен 137 градусов

ответ: 137градусов

Объяснение:

Наружные накрест лежащие углы

Для решения данной задачи, нам понадобятся понятия о параллельных прямых и свойства углов, образованных параллельными прямыми.

Перед тем как решить задачу, давайте вспомним некоторые основные свойства параллельных прямых:
1. У параллельных прямых соответствующие углы равны.
2. У параллельных прямых смежные углы дополняются до 180 градусов.

В задаче говорится, что прямые n и k параллельны. Это значит, что мы можем использовать свойства параллельных прямых для решения.

Обратим внимание на изображение, приложенное к задаче. Мы видим две параллельные прямые - n и k, а также два угла - угол 1 и угол 2. Угол 2 равен 137 градусов.

Воспользуемся свойством углов, образованных параллельными прямыми. Угол 1 и угол 2 - это смежные углы, которые дополняются до 180 градусов.

Таким образом, мы можем записать уравнение:
Угол 1 + Угол 2 = 180 градусов

Подставляя известные значения, получаем:
Угол 1 + 137 градусов = 180 градусов

Чтобы найти угол 1, нужно из уравнения вычесть 137 градусов:
Угол 1 = 180 градусов - 137 градусов

Выполняя вычисления, получаем:
Угол 1 = 43 градуса

Таким образом, угол 1 равен 43 градуса.

Пожалуйста, обрати внимание, что ответ получен путем решения математического уравнения и использования свойств параллельных прямых и смежных углов.