Прямоугольник вписан внутри эллипса 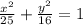Учитывая, что две стороны прямоугольника проходят через фокусы эллипса. Рассчитайте площадь прямоугольника.

Для заданного эллипса а= 5 и в = 4.

Расстояние от оси до фокуса с = √(а² - в²) = √(25 - 16) = √9 = 3.

Фокальный параметр этого эллипса находим по формуле:

р = в²/а = 16/5 = 3,2.

Отсюда определяем размеры прямоугольника, вписанного в эллипс.

Высота Н = 2р = 2*3,2 = 6,4, длина L = 2c = 2*3 = 6/

ответ: S = 6.4*6 = 38.4 кв.ед.