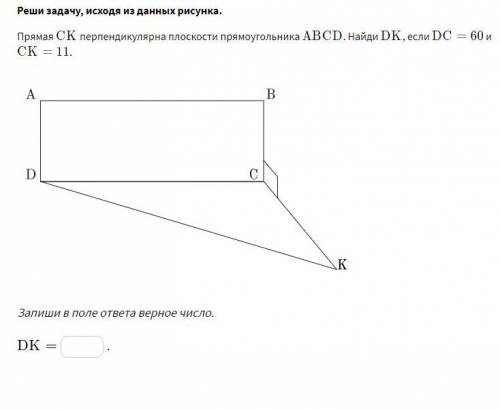
Прямая CKCK перпендикулярна плоскости прямоугольника ABCDABCD . Найди DKDK , если DC=60DC=60 и CK=11CK=11 . Запиши в поле ответа верное число.

DK =DK=

Чтобы решить эту задачу, нам нужно использовать свойство перпендикулярности прямых и знание о прямоугольниках. Когда прямая CK перпендикулярна к плоскости прямоугольника ABCD, она проходит через вершину C и пересекает противоположную сторону AD в точке K. Мы знаем, что DC = 60 и CK = 11. Чтобы найти DK, нам нужно найти длину отрезка KD. Первое, что мы можем сделать - это найти длину отрезка KC. Для этого мы можем использовать теорему Пифагора в прямоугольном треугольнике CKD. Используем теорему Пифагора: KC^2 + KD^2 = CK^2 Подставляем известные значения: KC^2 + KD^2 = 11^2 Теперь нам нужно найти длину отрезка KC. Мы можем это сделать, используя свойство прямоугольника, которое гласит, что противоположные стороны прямоугольника равны. Таким образом, DC = KC = 60. Подставляем и находим значения: 60^2 + KD^2 = 11^2 Решаем уравнение: 3600 + KD^2 = 121 KD^2 = 121 - 3600 KD^2 = -3479 Мы получили отрицательное число, что означает, что отрезок DK не существует. Таким образом, ответ на задачу - отрезок DK не существует.