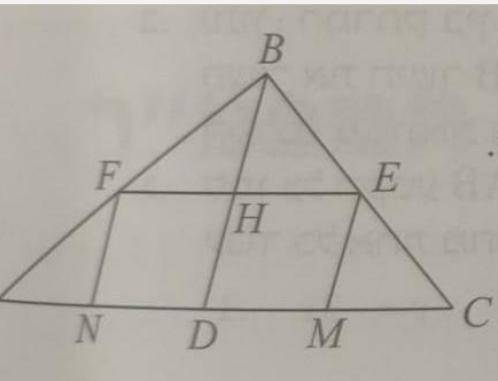
Прямая BD медиана к гипотенузе прямоугольного треугольника ABC. FM и EM это серединные линии в треугольниках BCD ABD соответственно. 1. Доказать что EHDM это ромб.
2. Дано: AB = 16 BC = 12 узнайте периметр ромба EHDM
Другие вопросы по теме Геометрия
Популярные вопросы
- За 4класс: арман задумал число,увеличил его в 7раз,вычел 27,уменьшил...
1 - Кто нибудь напишите сочинение на казахском если бы я был батыром желательно...
2 - Решить неравенство: |х^2+х-5| 3х...
1 - 1)напишите три трёзначных числа с цифр 1 и 3 (цифры могут повторяться...
3 - Нужно 10 вопросительныж предл, и 10 утрицательных!...
1 - Если можете то решите уравнением 4.1 - а) 3х = 6 4.2 - а) 4х + 20 =...
1 - Составте список эффективного общения,расположив их по степени важности...
3 - Сочинение по на тему праведник и защитник земли...
1 - Injured people were taken hospital a. a б. an c. -...
2 - Укажи слово, в приставке которого пишится буква а. расписание. подумать....
1
1
BD=1/2AC=DC => треугольник ВDC - равнобедренный
ЕМ - средняя линия => ЕМ=1/2ВD
EM - средняя линия => ВН=HD
по т. Фалеса ВЕ=ЕС => EH - средняя линия и EH=1/2DC
BD=DC => EH=EM
средние линии параллельны основаниям треугольников => ЕМ || ВD и ЕН || DC => DHEM - параллелограмм => НD=EM и НЕ=DM, а ЕН=ЕМ => НD=EM=НЕ=DM => это ромб
2
по теореме Пифагора
АС²=АВ²+ВС²
АС²=16²+12²=256+144=400
АС=20
BD=1/2AC (из доказательства 1) => BD=1/2*20=10
BH=HD (из доказательства 1) => HD=1/2BD=1/2*10=5
Phdme=HD+DM+ME+HE=4HD (т.к. НDME - ромб)
Phdme=4*5=20