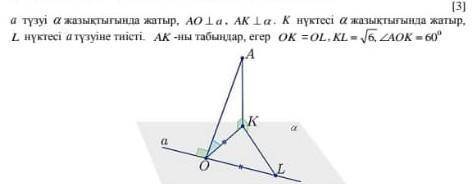
Прямая а лежит в плоскости а. A перпендикуляр a, AK перпендикуляр a. Точка K лежит на плоскости a, точка L должна лежать на прямой a. Найдите AK, если OK = OL, KL = корень 6, <AOK = 60 °​

Для начала, вспомним некоторые определения и свойства.

Прямая - это бесконечно продолжаемая фигура, которая не имеет ни ширины, ни длины.

Перпендикулярные прямые - это две такие прямые, которые пересекаются под прямым углом (90 градусов).

Теперь, давайте разберемся с данными из вопроса. Возьмем отрезок OK и на нем отметим точку M, такую что OM = OK. В результате получается равнобедренный треугольник OMK. Так как OK = OL, то отрезок OL также будет равен отрезку OK.

Нам дан угол AOK, равный 60 градусов. Так как OK = OL и треугольник OMK равнобедренный, то угол OKM также будет равен 60 градусов.

Обратим внимание, что угол OKM образуется между прямыми a и AK, которые перпендикулярны. В результате получается, что угол KAL также будет равен 60 градусам.

Теперь, посмотрим на треугольник AKL, в котором угол KAL равен 60 градусам.

Дано, что KL = √6. Нам нужно найти длину отрезка AK.

Для решения этой проблемы воспользуемся теоремой косинусов, которая гласит:

a^2 = b^2 + c^2 - 2bc * cos(A),

где a, b, c - длины сторон треугольника, A - угол между сторонами b и c.

Применим эту формулу к треугольнику AKL, где AK - сторона a, KL - сторона b, KL - сторона c и угол KAL - угол A. Таким образом, получим:

AK^2 = (√6)^2 + (√6)^2 - 2 * √6 * √6 * cos(60)

AK^2 = 6 + 6 - 2 * 6 * 1/2

AK^2 = 12 - 6

AK^2 = 6

Извлекая квадратный корень обеих сторон, получим:

AK = √6

Таким образом, длина отрезка AK равна √6.