Привет всем
Найти пары параллельных прямых и доказать их параллельность
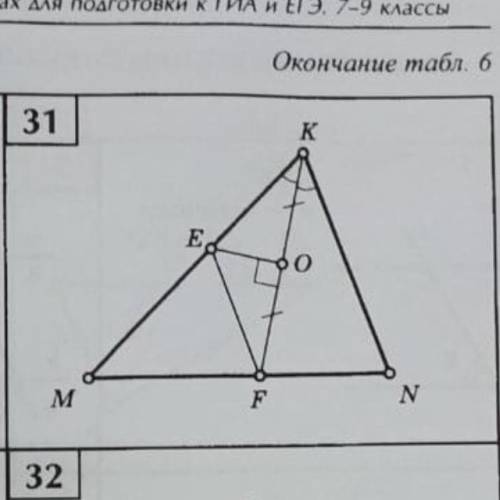
Другие вопросы по теме Геометрия
Популярные вопросы
- Постройте в одной системе координат графики функцией у=-2х+4 и у...
2 - Составить : цена 9 тенге, цена 72 тенге, количество одинаковое стоимость...
2 - Эксперимент со свечей 3 класс , что получится если зажечь свечу...
3 - 11.мақсат бағыныңқылы сабақтас құрмалас сөйлемнің сұрағын көрсетіңіз....
3 - Кто записывал первые летописи ? зарание !...
2 - Напишите отзыв по рассказу ,,подвиг у дубосекова...
1 - Наибольшее количество пятизначный является самым маленьким из пяти...
1 - Длина волны равна36 м ширина 5 высота4. метров найти площадь стены...
3 - Втреугольнике kmb угол m равен 90 градусов,кв=10,вм=8.найдите тангенс...
2 - Таня вышла из дома на 20 мин раньше мамы. через какое время мама...
3
В задаче нам нужно найти пары параллельных прямых и доказать их параллельность. Для начала, давай разберемся, что значит быть параллельными прямыми.
Две прямые называются параллельными, если они не пересекаются и расположены в одной плоскости. Если две прямые параллельны, то угол между ними будет равен нулю.
Посмотрим на данное изображение. Мы видим четыре прямые. Для того чтобы найти пары параллельных прямых, нужно найти две прямые, которые не пересекаются и похожи по направлению. Также, если они параллельны, угол между ними будет равен нулю.
Визуально, мы можем сделать предположение, что прямые AB и CD параллельны, так как они выглядят примерно одинаково и угол между ними кажется почти равным нулю. Для того чтобы убедиться в нашем предположении, нам нужно провести доказательство.
Мы можем провести два прямых участка AD и BC, так как они уже существуют на нашем рисунке.
1. Возьмем угол ADC. Обозначим его за α.
2. Возьмем теперь угол BCD. Обозначим его за β.
3. Доказательство будет заключаться в том, чтобы показать, что α = β.
Воспользуемся фактом, что сумма углов внутри треугольника равна 180 градусов. Поэтому можем записать следующее:
α + угол A + угол C = 180 градусов (1)
β + угол B + угол C = 180 градусов (2)
Но у нас есть дополнительная информация о треугольнике ABC. Это прямой угол на вершине C, кода между прямыми участками AD и BC равен 90 градусов. Запишем это:
угол A + угол B = 90 градусов (3)
Мы можем использовать уравнение (3) для упрощения уравнений (1) и (2):
α + 90 градусов = 180 градусов (4)
β + 90 градусов = 180 градусов (5)
Теперь мы можем решить эти уравнения:
α = 180 градусов - 90 градусов = 90 градусов
β = 180 градусов - 90 градусов = 90 градусов
У нас получилось, что α = β = 90 градусов. Это означает, что углы ADC и BCD равны между собой.
Так как углы, образованные прямыми AD и BC, равны, мы можем сделать вывод, что AD и BC параллельны. Таким образом, пара прямых AB и CD является параллельными.
Мы провели доказательство, что пары прямых AB и CD являются параллельными, используя свойство равенства углов. Надеюсь, этот ответ был полезным для тебя! Если у тебя есть еще вопросы, не стесняйся задавать их.