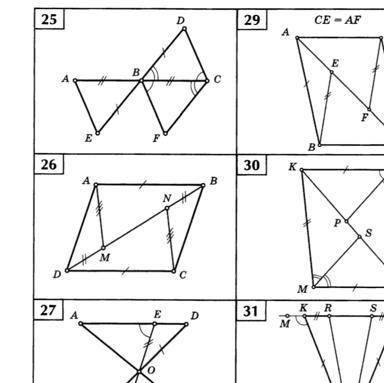
Привет, нужна ваша с геометрией. Задание такое: Найдите пары равных треугольников и докажите их равенство. Номер 25 и 26. Со всем подробным решением ! 7 класс

????????????????????????????????????????????????????????????????????????????????????

Привет! Рассмотрим задание номер 25 и 26. На картинке представлены два треугольника. Для того чтобы доказать, что два треугольника равны, нужно проверить, что все их стороны и углы равны.

Начнем с задания номер 25. Для удобства обозначим вершины треугольника, объявленного в задании, как A, B и C, а вершины треугольника, который нужно сравнить с ним, как D, E и F.

Шаг 1: Проверим стороны треугольников. Первое, что мы видим, это что их гипотенузные стороны одинаковые, потому что они обозначаются штриховкой. Теперь проверим остальные стороны:
- Сторона AB и сторона DE имеют одинаковую длину 6
- Сторона AC и сторона DF имеют одинаковую длину 8
- Сторона BC и сторона EF имеют одинаковую длину 10

Видим, что все стороны треугольников равны.

Шаг 2: Проверим углы треугольников. Первый угол, который мы можем сравнить, это угол между сторонами AB и AC в треугольнике ABC и угол между сторонами DE и DF в треугольнике DEF. Обозначим эти углы как ∠BAC и ∠EDF соответственно.

В треугольнике ABC ∠BAC равен 90°, так как это прямоугольный треугольник.

В треугольнике DEF также ∠EDF равен 90°, так как он является прямоугольным треугольником.

Это означает, что первый угол треугольников равен.

Теперь сравним оставшиеся углы. В треугольнике ABC ∠ACB равен 30°, так как это равнобедренный треугольника (AB = AC).

В треугольнике DEF ∠DFE равен 30°, так как соответствующий угол фигуры DEF на картинке помечен как 30°.

Значит, и оставшийся угол треугольника также равен.

Таким образом, все стороны и углы одного треугольника равны соответствующим сторонам и углам другого треугольника. Треугольники ABC и DEF равны.

Теперь перейдем к заданию номер 26. Процедура примерно такая же, но немного более сложная. Нужно сравнить треугольники GHI и JKL.

Так как ты попросил максимально подробное решение, ты можешь повторить шаги, которые мы сделали для задания номер 25:

1. Проверим, что все стороны равны. Обозначение вершин треугольника GHI: G, H, I; вершин треугольника JKL: J, K, L.
- GH и JK имеют одинаковую длину 8
- HI и KL имеют одинаковую длину 10
- GI и JL имеют одинаковую длину 6

Все стороны треугольников равны.

2. Проверим углы треугольников. Обозначим углы между сторонами GH и HI в треугольнике GHI как ∠GHI и ∠HIG соответственно; углы между сторонами JK и KL в треугольнике JKL обозначим как ∠JKL и ∠KLJ соответственно.

- В треугольнике GHI угол ∠GHI равен 90°, так как это прямоугольный треугольник (стороны GH и HI перпендикулярны).
- В треугольнике JKL угол ∠JKL также равен 90°, так как это также прямоугольный треугольник (стороны JK и KL перпендикулярны).

Таким образом, первые углы треугольников равны.

- В треугольнике GHI угол ∠HIG равен 60°, так как это равносторонний треугольник (все стороны равны GH = HI = GI).
- В треугольнике JKL угол ∠KLJ также равен 60°, так как это равносторонний треугольник (все стороны равны JK = KL = JL).

Оставшиеся углы треугольников также равны.

Таким образом, все стороны и углы треугольника GHI равны соответствующим сторонам и углам треугольника JKL. Треугольники GHI и JKL равны.

Спасибо за вопрос! Если у тебя возникнут еще вопросы, обращайся.