При каком значении m и n прямые параллельны?
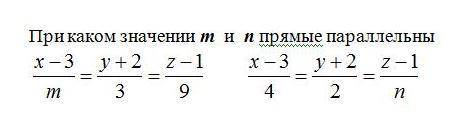
Популярные вопросы
- Мячик подбросили вертикально вверх с начальной скоростью 7,7 м/с. с точностью...
2 - Вариант 21. начертіпте координатную прямую, приняв за единичныйотрезок пять...
1 - Существует ли log1 в 5 степени?...
2 - Сочинение рассуждение на тему мцыри как свободолюбивый герой...
1 - Запишите ключевые и словасасочитание о погоде...
2 - Ii вариант1. определите, где содержится больше атомов и отметьте знаками...
1 - 1. за 1 платишь рубль , за 12 - 2 рубля , за 400 - 3 рубля. что это? 2....
2 - 50 ! ! только верно решите, умоляю.те кто не знают, как решать такое, проходите...
2 - Решить 3 1. в вместимостью 26000 см( в кубе) находится газ под давлением...
1 - Небольшая работа зделайте много...
2
Направляющий вектор прямой можно получить из ее уравнения. В данном случае, уравнение прямой a можно записать в виде y = mx, где m - это коэффициент пропорциональности, а n - это свободный член (то есть значение y, когда x = 0).
Теперь нам нужно найти направляющий вектор прямой a и прямой b и проверить, когда они пропорциональны.
Для прямой a:
Направляющий вектор a можно представить в виде (1, m), так как если x растет на 1 (изменение x = 1), то y растет на m (изменение y = m*1 = m).
Для прямой b:
Направляющий вектор b можно представить в виде (1, n), так как если x растет на 1 (изменение x = 1), то y растет на n (изменение y = n*1 = n).
Теперь, чтобы прямые a и b были параллельны, их направляющие векторы должны быть пропорциональны. Это означает, что (1, m) должен быть пропорционален (1, n).
Векторы (1, m) и (1, n) пропорциональны, если они имеют одинаковое отношение координат. Поэтому, чтобы узнать, при каких значениях m и n прямые параллельны, нужно установить равенство:
1/m = 1/n
Теперь произведем кросс-умножение:
n = m
Таким образом, прямые a и b будут параллельными, когда m = n.