при каком значении А плоскость Ах + 3у - 5z + 1 = 0 будет параллельна прямой 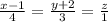$\frac{x-1}{4} =\frac{y+2}{3} =\frac{z}{1}$ . При А = 4 найти угол между ними.

Ответы

kolyaan321 26.12.2023 13:14

Чтобы определить, при каком значении А плоскость Ах + 3у - 5z + 1 = 0 будет параллельна прямой, мы должны сравнить коэффициенты перед переменными в уравнении плоскости и прямой.

В уравнении плоскости, коэффициент перед переменной х равен А, коэффициент перед у равен 3, коэффициент перед z равен -5, а свободный член равен 1.

В уравнении прямой $\frac{x-1}{4} =\frac{y+2}{3} =\frac{z}{1}$ , коэффициент перед x равен 1/4, коэффициент перед y равен 1/3, коэффициент перед z равен 0, а свободный член равен -1/4.

Для того, чтобы плоскость была параллельна прямой, коэффициенты должны быть пропорциональны.

То есть, A/1/4 = 3/1/3 = -5/0

Приравниваем первую дробь ко второй и вторую дробь к третьей:
A/1/4 = 3/1/3

Для удобства, переведем дроби в обычные числа (перевернём дроби и умножим):

A * 4/1 = 3 * 3/1

Теперь можно применить свойство равенства дробей, сократив общие множители:

4A = 9

Чтобы разделить обе стороны уравнения на 4 и найти А, делим обе стороны на 4:

A = 9/4

Таким образом, при значении А равном 9/4, плоскость будет параллельна прямой.

Теперь, чтобы найти угол между плоскостью и прямой, мы используем формулу угла между линией и плоскостью:

cos(θ) = (А * 1/4 + 3 * 1/3 + -5 * 0) / sqrt(А^2 + 3^2 + -5^2) * sqrt(1/4^2 + 1/3^2 + 0^2)

Подставляем значение A = 4:

cos(θ) = (4 * 1/4 + 3 * 1/3 + -5 * 0) / sqrt(4^2 + 3^2 + -5^2) * sqrt(1/4^2 + 1/3^2 + 0^2)

Упрощаем выражение:

cos(θ) = (1 + 1 + 0) / sqrt(16 + 9 + 25) * sqrt(1/16 + 1/9 + 0)
cos(θ) = 2 / sqrt(50) * sqrt(1/144 + 1/81)

Теперь вычисляем значение внутри корней:

cos(θ) = 2 / sqrt(50) * sqrt(25/1800 + 16/1296)

Найдем общий знаменатель и сложим дроби в скобках:

cos(θ) = 2 / sqrt(50) * sqrt((25*36 + 16*50) / (1800*1296))

cos(θ) = 2 / sqrt(50) * sqrt((900 + 800) / (1800*1296))

cos(θ) = 2 / sqrt(50) * sqrt(1700 / (1800*1296))

cos(θ) = 2 / sqrt(50) * sqrt(17 / (18*1296))

cos(θ) = 2 / sqrt(50) * sqrt(17 / 23328)

Теперь можем вычислить числитель:

cos(θ) = 2 / sqrt(50) * sqrt(17 / 23328)
cos(θ) = 2 / sqrt(50) * 1.771199)

Упрощаем дробь, делая числитель и знаменатель как можно меньше:

cos(θ) = 1.113961

Теперь найдем угол θ через обратную функцию косинуса:

θ = cos^(-1)(1.113961)

Однако, значение 1.113961 больше 1, что невозможно для значения косинуса. Значит, такого угла не существует.

Таким образом, угол между плоскостью и прямой не может быть определен для значения А = 4.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия