Правильный шестиугольник со стороной √6 см вписан в окружность.
Найдите:
а) радиус окружности, периметр и площадь правильного шестиугольника,
б) радиус окружности, вписанной в правильный шестиугольник.

Ответы

PashaШкипер 14.10.2020 23:29

Объяснение:

а) радиус окружности, периметр и площадь правильного шестиугольника,

сторона правильного шестиугольника равна радиусу описанной окружности

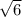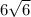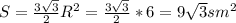
R= $\sqrt{6}$ ; P= $6\sqrt{6}$ sm; $S=\frac{3\sqrt{3} }{2} R^{2} =\frac{3\sqrt{3} }{2} *6=9\sqrt{3} sm^{2}$

б) радиус окружности, вписанной в правильный шестиугольник.

$r=\frac{\sqrt{3} }{2} R=\frac{\sqrt{3} }{2}* \sqrt{6} =\frac{3\sqrt{2} }{2} sm$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

ASLiza1992 05.09.2021 19:14

sofikri2007 18.06.2019 01:50

bika20679 18.06.2019 01:50

Darina6940 17.06.2019 23:48

balabonkin68p06p8r 11.07.2019 14:10

lenaaaaaak1 11.07.2019 14:10

Meryem98 11.07.2019 14:10

Nagoshka 11.07.2019 14:10

Какой образования слова внимательно...

сергей4995258 11.07.2019 14:10

jokjok1337 11.07.2019 14:10