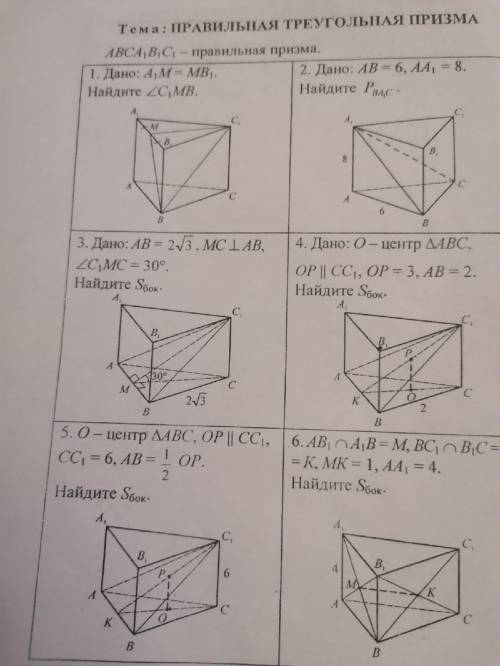
Правильная треугольная призма
Другие вопросы по теме Геометрия
Популярные вопросы
- Речевая характеристика самсона вырина. сегодня...
1 - Если на прямой взять 6 точек,то сколько всего получится отрезков,концами...
3 - Сравни поставить знак больше меньше или равно 6 м,59дм...
3 - Прочитай и определи значений выделенных слов почему береза сравнивается...
2 - Если я был рыбаком в древнем египте. сочинение...
3 - Выберите правильное написание союзов и наречий с частицами. 1....
2 - При первом сжатии длина пружины изменилась на -1,2 см. при втором...
3 - Рассказ как папа дружил с девочкой придумай свой заголовок к тексту...
3 - Как проверить букву о в слове заполыхала...
2 - Вычислите , чему равна разность 2400м-0,8км...
2
Перед тем, как перейти к решению, давайте определим, что такое правильная треугольная призма. Правильная призма - это призма, у которой основания являются правильными многоугольниками (такими, у которых все стороны и углы равны между собой) и боковые грани являются равными равнобедренными треугольниками (треугольниками, у которых две стороны равны).
У нас дана трехугольная призма, у которой основание - это правильный треугольник, а боковые грани - равнобедренные треугольники.
Давайте решим задачу пошагово.
Шаг 1: Найдите площадь основания треугольной призмы.
Для этого нам понадобится найти площадь правильного треугольника. Формула для нахождения площади правильного треугольника это Площадь = (сторона^2 * sqrt(3))/4, где "сторона" - это длина стороны треугольника. На основании данной формулы, вы можете использовать данные изображения, чтобы вычислить площадь основания.
Шаг 2: Найдите площадь одной из боковых граней.
Для этого вам понадобится найти площадь равнобедренного треугольника. Формула для нахождения площади равнобедренного треугольника это Площадь = (база * высота)/2, где "база" - это длина основания треугольника, а "высота" - это перпендикуляр, опущенный из вершины треугольника на его основание. Воспользуйтесь данными изображения, чтобы вычислить площадь одной из боковых граней.
Шаг 3: Найдите общую площадь поверхности призмы.
Для этого умножьте площадь одной из боковых граней на количество таких граней (в данном случае их 3) и добавьте площадь основания. Общая площадь поверхности призмы будет равна сумме площади основания и утроенного значения площади одной из боковых граней.
Шаг 4: Найдите объем призмы.
Для этого умножьте площадь основания на высоту призмы. Воспользуйтесь данными изображения, чтобы вычислить объем призмы.
Опираясь на пошаговое решение, школьнику будет легче понять, как найти площадь и объем правильной треугольной призмы. Данный подход поможет школьнику лучше разобраться в математической задаче и решить ее.