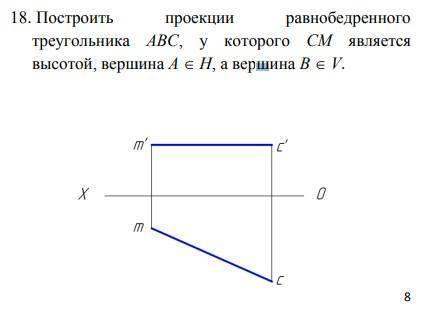
Построить проекции равнобедренного треугольника АВС, у которого СМ является
высотой, вершина А э Н, а вершина В э V.с обьяснением

Для начала, давайте определим, что такое проекции. Проекции - это изображения фигуры на плоскости, которые получаются, когда фигуру перпендикулярно проецируют на плоскость.

Из условия задачи видно, что треугольник АВС является равнобедренным и СМ - это его высота. Нам нужно построить проекции этого треугольника.

Для начала построим высоту СМ. Высота всегда проходит через вершину угла треугольника и перпендикулярна стороне, на которую она опущена. В данном случае, высота СМ перпендикулярна стороне АВ и проходит через вершину С. Построим прямую, проходящую через С, перпендикулярно стороне АВ, и обозначим точку пересечения этой прямой с стороной АВ как М.

Теперь, чтобы построить проекции треугольника, нам нужно перпендикулярно от точек А и В на сторону МС провести линии, которые будут пересекать соответствующие стороны треугольника АВС. Таким образом, мы получим две проекции треугольника - одну для вершины А и одну для вершины В.

Давайте начнем с построения проекции для вершины А. Проведем перпендикулярно от точки А на сторону МС и обозначим точку пересечения этого перпендикуляра со стороной СВ как К.

Теперь мы знаем, что треугольник АКМ - равнобедренный, потому что у него две стороны равны - АК равен МК и АМ равен ММ (так как М - это середина стороны СВ по условию задачи).

Построим проекцию для вершины А, проводя прямую от точки А до точки К.

Теперь перейдем к построению проекции для вершины В. Аналогично, проведем перпендикулярно от точки В на сторону МС и обозначим точку пересечения этого перпендикуляра со стороной АС как L.

Треугольник ВЛС также будет равнобедренным, потому что ВЛ и СЛ равны (как медианы равнобедренного треугольника) и ВВ равно СВ (потому что М - это середина стороны АС по условию задачи).

Построим проекцию для вершины В, проводя прямую от точки В до точки Л.

Теперь у нас есть две проекции: АК и BЛ. Эти проекции представляют собой изображения вершин треугольника АВС на стороне МС.

Надеюсь, что объяснение и пошаговое решение помогут вам понять, как построить проекции равнобедренного треугольника АВС, у которого СМ является высотой, вершина А находится в Н, а вершина В находится в V.