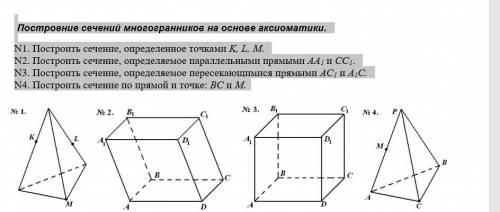
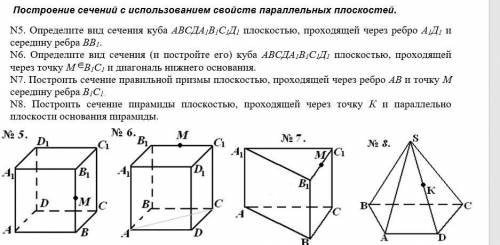
Построение сечений многогранников на основе аксиоматики. N1. Построить сечение, определенное точками K, L, M.
N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1.
N3. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С.
N4. Построить сечение по прямой и точке: BC и М.

Добрый день! Для построения сечений многогранников с использованием аксиоматики, нам необходимо знать некоторые основные понятия и правила геометрии. Давайте рассмотрим каждый вопрос по отдельности и найдем решение для каждого из них. N1. Построить сечение, определенное точками K, L, M. Нам даны точки K, L и M, и мы должны построить сечение многогранника (представленного на рисунке) через эти точки. Для этого следует прокатить плоскость через эти три точки, чтобы она пересекла многогранник. Строим плоскость, проходящую через точки K, L и M. На рисунке показан способ построения такой плоскости. [img1] Получившаяся плоскость будет сечением многогранника. N2. Построить сечение, определяемое параллельными прямыми АА1 и СС1. В этом случае нам даны две параллельные прямые АА1 и СС1. Чтобы построить сечение, необходимо взять плоскость, которая будет параллельна этим двум прямым, и прокатить ее через многогранник. Строим такую плоскость, как показано на следующем рисунке. [img2] Получившаяся плоскость будет сечением многогранника. N3. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С. В этом случае нам даны две прямые АС1 и А1С, которые пересекаются. Для построения сечения мы должны прокатить плоскость через эти две прямые таким образом, чтобы она пересекла многогранник. Вот как это можно сделать: 1. Строим пересечение прямых АС1 и А1С, чтобы найти точку пересечения. Обозначим эту точку как Р. 2. Затем построим высотку из точки Р на прямую ВВ1 многогранника: [img3] 3. Наконец, мы проводим плоскость через точку Р и параллельно прямым АС1 и А1С. Эта плоскость будет сечением многогранника. N4. Построить сечение по прямой и точке: BC и М. В данном случае нам дана прямая BC и точка М, и мы должны построить сечение, проходящее через эту прямую и точку. Вот как это можно сделать: 1. Строим перпендикуляр к прямой BC из точки М. Обозначим точку пересечения как N. 2. Теперь проводим прямую через точки N и М: [img4] 3. Получившаяся прямая будет лежать в плоскости, проходящей через прямую BC и точку М. Эта плоскость будет сечением многогранника. Вот таким образом можно построить сечения многогранников на основе аксиоматики, используя данную информацию. Если у вас остались вопросы или нужно дополнительное объяснение, пожалуйста, не стесняйтесь задавать их. Я готов помочь!