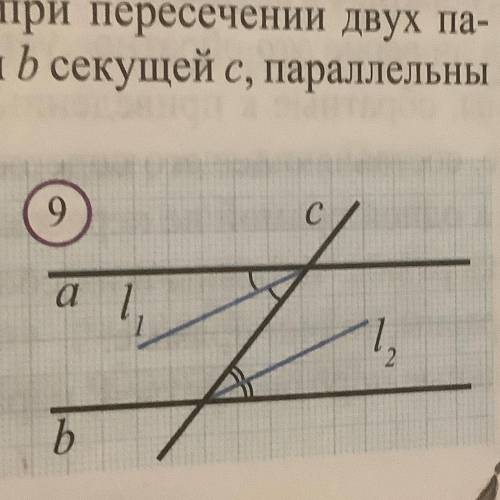
Покажите, что биссектрисы накрест лежащих углов, получающихся при пересечении двух параллельных прямых а и b секущей с, параллельны

Для начала, давайте разберем некоторые основные понятия:

- Биссектриса угла - это линия, которая делит угол на два равных по величине угла.
- Угол биссектрисы - это угол, образованный биссектрисой и одной из сторон исходного угла.

Данная задача предлагает нам рассмотреть пересечение двух параллельных прямых a и b секущей c. После пересечения образуются четыре угла: два внутренних и два внешних. Нам нужно показать, что биссектрисы накрест лежащих углов параллельны.

Для решения задачи мы можем использовать свойство параллельных прямых: если две прямые a и b параллельны и пересекаются с третьей (в данном случае секущей) прямой c, то сумма взаимно дополняющих углов равна 180 градусов.

Давайте обратимся к изображению. Пусть P и Q - точки пересечения секущей прямой c со сторонами параллельных прямых a и b соответственно.

Посмотрим на углы APQ и BPQ.
- Угол APQ образован стороной PQ и биссектрисой угла APQ.
- Угол BPQ образован стороной PQ и биссектрисой угла BPQ.

Так как прямые a и b параллельны, угол APQ и угол BPQ являются взаимно дополняющими углами. То есть их сумма равна 180 градусов.

Теперь рассмотрим углы APQ и BPQ.
- Угол APQ образован стороной PQ и биссектрисой угла APQ.
- Угол BPQ образован стороной PQ и биссектрисой угла BPQ.

Так как угол APQ и угол BPQ также являются взаимно дополняющими углами, их сумма также равна 180 градусов.

Итак, мы доказали, что сумма углов APQ и BPQ равна 180 градусов. Это означает, что биссектрисы накрест лежащих углов при пересечении двух параллельных прямых a и b секущей c являются параллельными.

Оживив задачу: можно выбрать любую из двух пар биссектрис и провести их на графике. При этом можно будет видеть, что эти биссектрисы будут параллельны друг другу.

Надеюсь, данное объяснение помогло вам разобраться в задаче!