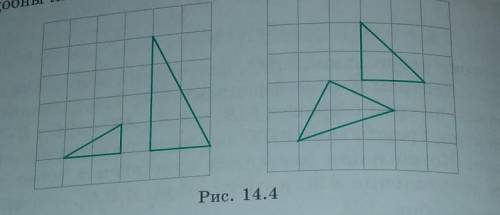
Подобны ли треугольники изображенные на рисунке 14.4​

Для того чтобы определить, являются ли треугольники на рисунке подобными, мы должны проверить, обладают ли они одинаковыми углами и пропорциональными сторонами.

Для начала, давайте обратим внимание на углы треугольников. В треугольнике ABC видим два угла вершины A. Обозначим эти углы как угол A1 и угол A2. В треугольнике DEF также видим два угла вершины D, обозначим их как угол D1 и угол D2. Нам нужно проверить, являются ли эти углы равными.

Углы A1 и D1 выглядят примерно одинаковыми, обозначим их как угол А1 = угол D1. Углы A2 и D2 также выглядят примерно одинаковыми, обозначим их как угол А2 = угол D2. Значит, углы вершин у этих треугольников равны.

Теперь проверим пропорциональность сторон. В треугольнике ABC сторона AB может соответствовать стороне DE, сторона BC может соответствовать стороне EF, и сторона AC может соответствовать стороне DF. Выглядит так, что соответствующие стороны пропорциональны.

Таким образом, мы можем заключить, что треугольники на рисунке 14.4 подобны, так как они имеют равные углы и пропорциональные стороны.

Надеюсь, это объяснение понятно для вас!