Подобие по первому признаку треугольников. ​

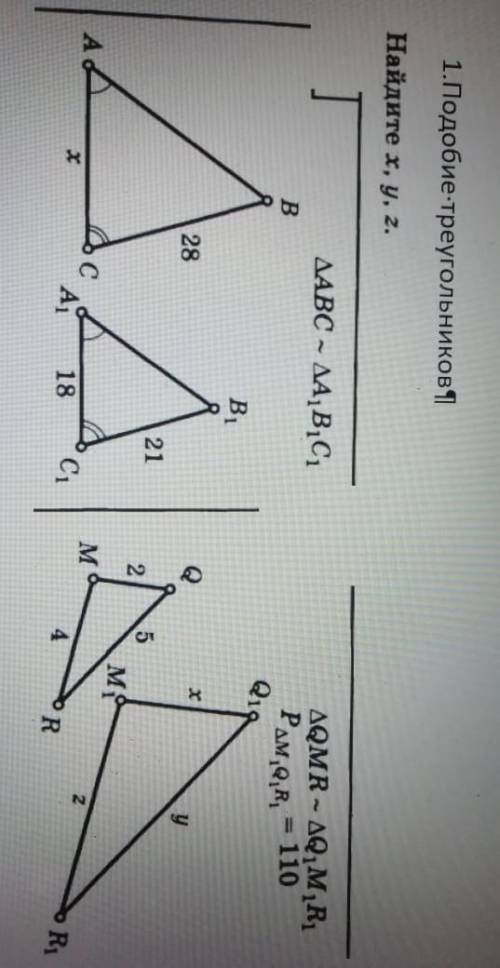
1) x = 24; 2) x = 20; y = 50; z = 40

Объяснение:

1) Если треугольники подобны, то отношения их сторон равны.

Составляем пропорцию 28/21 = x/18; x = 24

2) Отношения периметров подобных треугольников равны отношениям их сторон. Периметр QMR = 11, Q1M1R1 = 110.

QMR : Q1M1R1  = 110/11 = 10, следовательно отношения сторон тоже равно 10 ⇒ 5*10 = y (50), 4*10 = z (40), 2*10 = x (20).

Для того чтобы понять, что такое подобие треугольников по первому признаку, давай сначала вспомним, что такое подобные фигуры. Подобие означает, что две фигуры имеют одинаковую форму, но могут иметь разные размеры. То есть, их стороны пропорциональны.

Чтобы узнать, являются ли два треугольника подобными по первому признаку, мы должны проверить, будут ли их углы соответственными.

Для этого мы сравниваем углы одного треугольника с углами другого треугольника. Заметим, что каждый угол вершины треугольника обозначается как В, и каждый угол основание треугольника обозначается как О. В нашем случае, у нас есть углы В1, В2 и В3 для одного треугольника, и углы В1', В2' и В3' для другого треугольника.

Чтобы два треугольника были подобными по первому признаку, углы вершин одного треугольника должны быть равны углам вершин другого треугольника, а углы основания одного треугольника должны быть равны углам основания другого треугольника. То есть, В1 = В1', В2 = В2', В3 = В3', О1 = О1' и О2 = О2'.

Давай проверим это для данных треугольников. Углы В1 и В1' оба равны 90°, поэтому они соответствуют друг другу. Углы В2 и В2' оба равны 30°, опять же они соответствуют друг другу. Углы В3 и В3' оба равны 60°, также соответствуют друг другу. Теперь проверим углы основания. О1 и О1' оба равны 60°, а О2 и О2' оба равны 30°. Поэтому, все углы вершин и углы основания соответствуют друг другу.

Из этого следует, что данные треугольники являются подобными по первому признаку.

Этот способ проверки может быть использован для любых треугольников, где есть равенство углов вершин и углов основания. Равные углы показывают нам, что треугольники имеют одинаковую форму, а разница в размере сторон будет указывать на их подобие. Это полезное свойство, которое помогает нам анализировать и сравнивать треугольники и другие фигуры в геометрии.