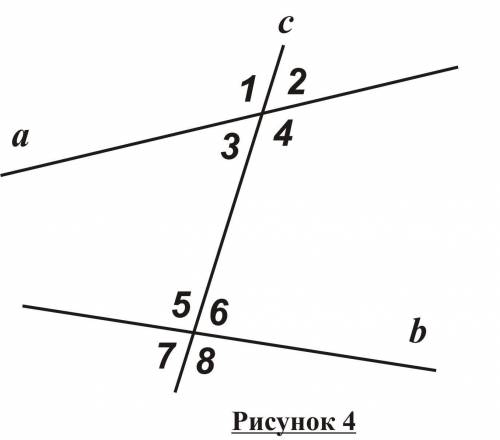
Почему углы при параллельных прямых и секущей равны только попарно? К примеру, Угол 1 и Угол 5 равны как соответственные. При том Угол 1 и Угол 7 равны как внутренние накрест-лежащие.

И, следовательно, Угол 5 равен углу 7? А если нет, то почему?

∠5 != ∠7 (они не равны друг другу).

Они будут равны друг другу только в случае, если секущая делит углы на равные части, каждый из углов прямой, тоесть каждый равен другому.

Кстати, в рисунке 4 прямые a & b — не параллельны друг другу.

Но предположим, что параллельны.

Да, ∠1 == <∠, так как они соотственные углы, но ∠1 != ∠7, один из них обязательно должен быть тупым, а другой — острым.

Но ∠1 например равен <8, так как ∠1 == ∠5 (как сооветственные углы), а ∠5 и ∠8 — вертикальные друг другу углы, тоесть равны, что и означает, что ∠1 == ∠8.

При параллельных прямых и секущей, есть всего лишь 2 определения углов, ибо они состоят только из вертикальных углов, и зависят только от 2 параллельных, и одной секущей.

В пример: ∠1 = 120°; ∠3 = 60° (так как они смежные углы, то их сумма должна равнятся 180°).

∠1 & ∠5 — соответственные углы, тоесть равны друг другу => ∠5 == ∠1 == 120°.

Но ∠5 одновременно вертикален с углом ∠8, что и означает, что: ∠1 == ∠5 == ∠8.

∠8 и ∠4 также являются парой соответсвенных углов, тоесть они равны друг другу, что и означает: ∠1 == ∠5 == ∠8 == ∠4.

Одни и те же действия с углом <3(60°).

Каждый угол зависит от другого.