По теореме синусов и косинусов решить треугольника авс, если а=6,3, b=6,3, угол с=54°.

Так как a = b = 6,3, то ΔАВС - равнобедренный

Углы при основании равнобедренного треугольника равны.

По теореме синусов находим АВ:

ответ:   ;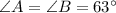  

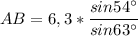
Добрый день! Разберем задачу по теореме синусов и косинусов.

Итак, у нас есть треугольник АВС, где стороны АС и ВС равны 6,3, а угол С равен 54°. Нам нужно найти оставшиеся стороны и углы треугольника.

1. Начнем с теоремы синусов, которая гласит:
a/sin(A) = b/sin(B) = c/sin(C)
где a, b, c - стороны треугольника, A, B, C - противоположные углы.

2. Нам известны стороны a и b, а угол C, поэтому мы можем найти третью сторону c, применив теорему синусов:
c/sin(C) = a/sin(A) => c = (a * sin(C)) / sin(A)

Подставляя известные значения, получим:
c = (6.3 * sin(54°)) / sin(A)

3. Теперь давайте найдем углы треугольника. Мы можем использоватьформулу косинусов:
c^2 = a^2 + b^2 - 2ab * cos(C)

Подставляя известные значения, получим:
(6.3)^2 = 6.3^2 + 6.3^2 - 2 * 6.3 * 6.3 * cos(54°)

После решения этого уравнения найдем значение угла А (или B):
cos(A) = (a^2 + c^2 - b^2) / 2ac

Подставляя известные значения, получим:
cos(A) = (6.3^2 + c^2 - 6.3^2) / (2 * 6.3 * c)

После нахождения cos(A), можно получить значение угла A через обратную функцию cos:
A = arccos(cos(A))

Аналогичным образом можно найти угол B.

Итак, школьник, чтобы решить данную задачу, необходимо:
1. Найти значение третьей стороны треугольника согласно теореме синусов.
2. Найти значения углов А и В с помощью формулы косинусов.

Надеюсь, это объяснение поможет вам лучше понять, как решить задачу по теореме синусов и косинусов.