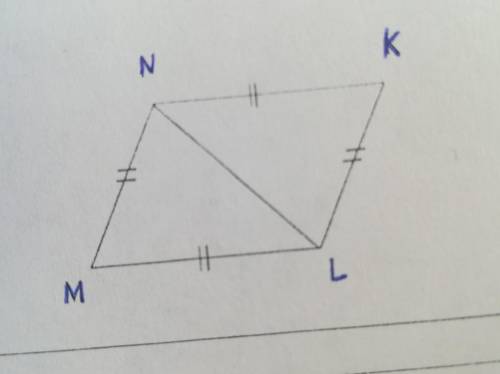
По готовому рисунку докажите, что MN || KL.

Хорошо, давайте рассмотрим данный рисунок и докажем, что MN || KL.

Для начала, давайте обозначим имена точек на рисунке. Вершина слева вверху обозначена буквой A, вершина внизу слева обозначена буквой B, вершина внизу справа обозначена буквой C, а вершина справа вверху обозначена буквой D.

Теперь, обратим внимание на отрезок AC и его продолжение MN. Заметим, что отрезок AC и отрезок MN являются диагоналями равнобедренной трапеции ABCD. Значит, они расположены в одной плоскости и их продолжения параллельны.

Теперь, обратим внимание на отрезок BD и его продолжение KL. Заметим, что отрезок BD и отрезок KL являются диагоналями параллелограмма ABCD. По свойству параллелограмма, диагонали параллелограмма делятся пополам. Значит, точка пересечения диагоналей точка O является серединой отрезка KL.

Теперь, обратим внимание на треугольники ABM и ADC. Заметим, что эти треугольники являются подобными, так как они имеют два равных угла - угол BAC и угол ACD и имеют общий угол BAD. Известно, что если два треугольника подобны, то соответственные стороны образуют параллельные прямые.

Теперь, зная что сторона BM соответствует стороне DC, а сторона MA соответствует стороне CD, можем сделать вывод, что отрезок MN параллелен отрезку AC.

Таким образом, мы доказали, что MN || KL, поскольку соответственные стороны подобных треугольников ABM и ADC параллельны.

Надеюсь, объяснение было понятным! Если у вас остались вопросы, пожалуйста, задайте их.