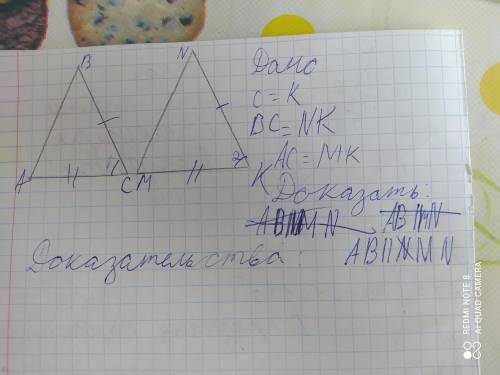
по геометрии задали я без углов не могу док-ва делать Если что C=K
AC=MK
BC=NK
Доказать :AB||MN АБ параллельно МН

Для решения данной задачи, нам понадобятся некоторые основные геометрические свойства и определения.

Для начала, давайте рассмотрим, что означает параллельность двух прямых. Две прямые AB и MN называются параллельными, если все точки одной прямой находятся на одинаковом расстоянии от другой прямой.

Теперь давайте разберемся с данными, которые нам даны.

У нас есть треугольник ABC и треугольник MKN.

Мы знаем, что AC = MK, что означает, что отрезок AC имеет ту же длину, что и отрезок MK. Это означает, что точка C лежит на отрезке MK.

Также у нас есть, что BC = NK, то есть отрезок BC имеет ту же длину, что и отрезок NK. Это означает, что точка C лежит на отрезке NK.

Исходя из этой информации, мы можем заключить, что точка C является общей точкой для отрезков MK и NK. То есть мы можем сказать, что вершина C лежит на прямой MN.

Итак, мы имеем следующее:

1. AC = MK (дано)
2. BC = NK (дано)
3. C лежит на прямой MN

Теперь рассмотрим треугольник ABC.

Для доказательства того, что AB || MN (прямые параллельны), нам понадобится теорема, которая гласит: "Если два отрезка, соединяющие две параллельные прямые с третьей прямой, равны между собой, то эти две прямые параллельны между собой".

Исходя из данной теоремы, нам нужно доказать, что AB и MN равны между собой.

Так как нам дано, что AC = MK и BC = NK, мы можем заметить, что AB = (AC + BC) и MN = (MK + NK).

Записав данное уравнение, получим AB = (AC + BC) и MN = (MK + NK).

Так как AC = MK и BC = NK, мы можем заменить значения в уравнении:

AB = (AC + BC) = (MK + NK) = MN

Таким образом, мы получаем AB = MN, что означает, что отрезки AB и MN равны между собой.

Исходя из теоремы, которую мы использовали ранее, если два отрезка, соединяющие две параллельные прямые с третьей прямой, равны между собой, то эти две прямые параллельны между собой.

Таким образом, мы можем заключить, что AB || MN (прямые параллельны).

Окончательно, чтобы доказать, что AB || MN, мы использовали следующие факты:

1. AC = MK (дано)
2. BC = NK (дано)
3. C лежит на прямой MN
4. AB = MN (доказано)

Надеюсь, ответ был понятен и полезен для тебя! Если у тебя еще есть какие-либо вопросы, не стесняйся задавать их.