по геометрии
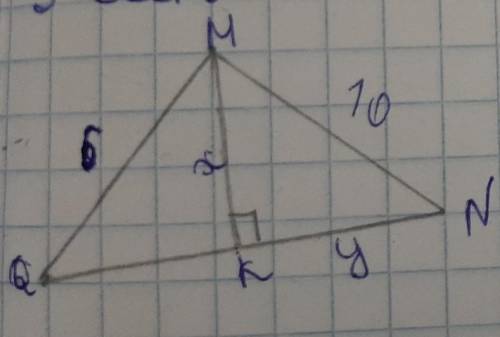
QN=12, QM=6, MN=10
KN, MK=?

​

Для решения данной задачи по геометрии, мы должны использовать теорему Пифагора и свойство треугольника. Сначала, давайте посмотрим на треугольник QMN. У нас есть три стороны: QN, QM и MN. Мы знаем, что QN = 12, QM = 6 и MN = 10. Теперь, используя теорему Пифагора, мы можем определить длину стороны QN: QN^2 = QM^2 + MN^2 QN^2 = 6^2 + 10^2 QN^2 = 36 + 100 QN^2 = 136 Теперь возьмем квадратный корень от обеих сторон, чтобы найти QN: QN = √136 Мы можем упростить это выражение: QN = √4 * √34 QN = 2√34 Итак, мы нашли, что длина стороны QN равна 2√34. Теперь давайте разберемся с треугольником KMN. Мы знаем, что KM это прямая, которая проходит через M и K, поэтому мы можем использовать свойство треугольника, чтобы дать нам информацию о длинах сторон этого треугольника. Мы знаем, что сторона QN длиннее стороны QM. Таким образом, сторона KN должна быть длиннее стороны KM. Теперь мы можем ответить на вопрос и найти длину стороны KN как KN = 2√34 + 6. Таким образом, мы можем заключить, что длина стороны KN равна 2√34 + 6, а длина стороны MK равна 6.