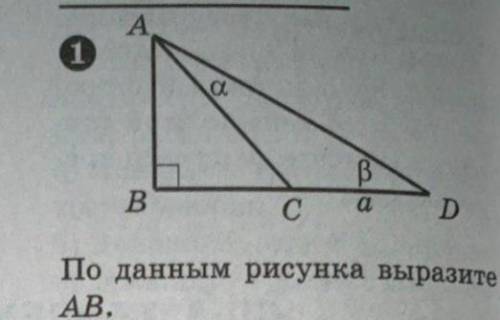
По данным рисунка выразите АВ?

Для того чтобы выразить АВ, необходимо использовать информацию, предоставленную на рисунке. На рисунке видно, что отрезок АВ представляет собой прямую линию, которая проходит через точку А и точку В.

Шаг 1: Определим координаты точек А и В. По декартовой системе координат, точка А имеет координаты (2, 1), а точка В имеет координаты (5, 4).

Шаг 2: Найдем уравнение прямой, проходящей через эти две точки. Для этого воспользуемся формулой уравнения прямой, которая выглядит следующим образом: y = mx + b, где m - это коэффициент наклона прямой, а b - это коэффициент сдвига (или y-пересечение).

Шаг 3: Вычислим значение коэффициента наклона m, используя формулу m = (y2 - y1) / (x2 - x1). В данном случае, координаты точки А - (2, 1), а координаты точки В - (5, 4). Подставив значения в формулу, получим: m = (4 - 1) / (5 - 2) = 3 / 3 = 1.

Шаг 4: Найдем значение коэффициента сдвига b, используя формулу b = y - mx. Подставив значения координат точки А в формулу, получим: b = 1 - 1 * 2 = 1 - 2 = -1.

Шаг 5: Теперь, когда у нас есть значения для коэффициента наклона m и коэффициента сдвига b, мы можем записать уравнение прямой в форме y = mx + b. Подставив значения m и b в уравнение, получим: y = x - 1.

Таким образом, уравнение прямой, проходящей через точки А и В, будет выглядеть следующим образом: y = x - 1. Это и будет выражением для отрезка АВ.