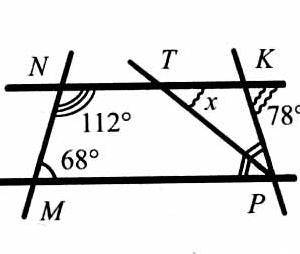
По данным рисунка найдите величину угла х.
Другие вопросы по теме Геометрия
Популярные вопросы
- Лентяй да шалопай два родных брата. хочешь есть калачи, - не лежи на...
3 - :сумма длин всех сторон прямоугольника равна 18 см.какими могут быть...
1 - Докажите .что корневище-видоизмененный побег...
3 - Лена с папой отправились к бабушке.они сели в 15часов,а приехали к бабушке...
2 - Заполнить массив из 25 элементов от -113 до 27. посчитать сумму и элементы...
1 - Предложите разделения смесей, состоящих: а) из железных и медных опилок...
2 - Вкакой строке указаны только газообразные вещества? вода, крахмал, соль,...
1 - Какие части света различают на земле?...
1 - Строение и функции сердечно-сосудистой системы. возрастные особенности....
3 - Миша задумал число, вычислил из него 7, прибавил 25, потом прибавил...
3
Наша задача состоит в том, чтобы найти значение угла x. Обратим внимание на то, что угол x находится напротив стороны длиной 15 см. Это означает, что данный треугольник является треугольником со сторонами 15 см, 10 см и x.
Теперь, для того чтобы найти значение угла x, воспользуемся теоремой косинусов. Согласно этой теореме, квадрат длины стороны, расположенной напротив угла, равен сумме квадратов длин оставшихся двух сторон минус удвоенное произведение длин этих двух сторон на косинус угла между ними.
В нашем случае, стороны треугольника имеют длины 15 см, 10 см и x, а угол между сторонами длиной 15 см и 10 см обозначен как x. Подставим эти значения в теорему косинусов:
15^2 = 10^2 + x^2 - 2 * 10 * x * cos(x)
Раскроем скобки и упростим:
225 = 100 + x^2 - 20x * cos(x)
Приравниваем к нулю:
x^2 - 20x * cos(x) + 125 = 0
Данное уравнение не имеет простых аналитических решений. Подставим его в компьютер или карманный калькулятор и найдем приближенные значения для x.
Другой способ решения подобных задач - использование геометрических построений. Мы видим, что треугольник прямоугольный, а стороны длиной 10 см и x находятся во вписанном треугольнике. Таким образом, мы можем использовать соотношение Пифагора для нахождения значения угла x:
10^2 + x^2 = 15^2
100 + x^2 = 225
x^2 = 125
x ≈ √125
x ≈ 11.18
Таким образом, величина угла x примерно равна 11.18 градусов.