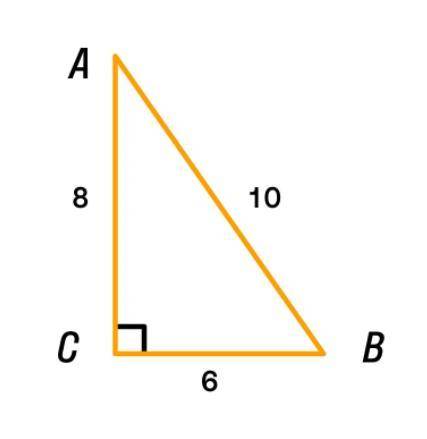
По данным рисунка найди sin a sin b cos a cos b tg a tg b

Для решения данной задачи нам потребуется знание основных тригонометрических функций - синуса, косинуса, тангенса.

На рисунке дан прямоугольный треугольник ABC, где углы соответствующие сторонам между A и B обозначены как a, а соответствующие сторонам между A и C обозначены как b.

Сначала найдем значения синуса, косинуса и тангенса для каждого из углов.

Для угла a:
sin a = противолежащая сторона / гипотенуза = AC / AB
cos a = прилежащая сторона / гипотенуза = BC / AB
tg a = противолежащая сторона / прилежащая сторона = AC / BC

Для угла b:
sin b = противолежащая сторона / гипотенуза = BC / AB
cos b = прилежащая сторона / гипотенуза = AC / AB
tg b = противолежащая сторона / прилежащая сторона = BC / AC

Теперь, зная значения синусов, косинусов и тангенсов для углов a и b, мы можем найти искомое произведение: sin a sin b cos a cos b tg a tg b.

sin a sin b cos a cos b tg a tg b = (AC / AB) * (BC / AB) * (AC / AB) * (BC / AC)

Заметим, что AC / AB встречается 2 раза, поэтому можно сократить это выражение:

sin a sin b cos a cos b tg a tg b = (AC / AB) * (BC / AB) * (BC / AC)
= (AC * BC * BC) / (AB * AB * AC)
= BC^2 / AB^2

Таким образом, ответ на вопрос "sin a sin b cos a cos b tg a tg b" равен BC^2 / AB^2.

Надеюсь, этот ответ понятен для школьника. Если остались какие-либо вопросы, пожалуйста, скажите.