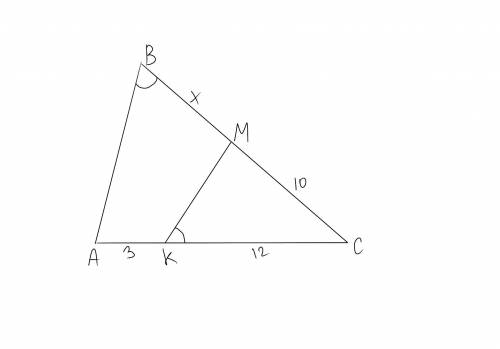
По данным на рисунке найдите BM

15

Объяснение:

10+15=25 180:25=7.2 каждый градус

ответ: 8.

Надеюсь )

Для нахождения значения BM, нам нужно использовать заданные данные на рисунке. Рисунок показывает треугольник ABC, и у нас есть информация о длинах отрезков AC, AB и BC.

В данном случае, чтобы найти длину отрезка BM, мы можем использовать теорему Пифагора, так как треугольник ABC является прямоугольным треугольником с прямым углом в вершине B.

Теорема Пифагора гласит, что для прямоугольного треугольника квадрат длины гипотенузы (в данном случае AB) равен сумме квадратов длин двух других сторон (AC и BC).

Из рисунка мы видим, что AC равно 6 и BC равно 8. Мы хотим найти длину BM.

Используя теорему Пифагора, мы можем записать это в виде уравнения:

AB^2 = AC^2 + BC^2

Заменив значения AC и BC, получим:

AB^2 = 6^2 + 8^2

AB^2 = 36 + 64

AB^2 = 100

Чтобы найти длину AB, мы можем извлечь квадратный корень из обеих сторон уравнения:

AB = sqrt(100)

AB = 10

Таким образом, длина отрезка AB равна 10.

Чтобы найти длину BM, мы можем поделить длину AB пополам:

BM = AB / 2

BM = 10 / 2

BM = 5

Таким образом, длина отрезка BM равна 5.